背景
这段时间做了些布料模拟相关的工作,实际内容是对 KawaiiPhysics 做了一些二次开发,使它满足美术表现效果。为什么要对 KawaiiPhysics 做二次开发呢?
美术比较习惯使用代理网格进行模拟工作流程,但是 UE5 里的 Chaos Cloth 始终达不到他们想要的效果,而且 Chaos 的开销还很大。于是拿来了 KawaiiPhysics,但 KawaiiPhysics 的效果实际上是针对单根骨骼,对相邻的骨骼缺少约束,更适合做短裙,中短发还有乳摇的效果。而我们项目里的衣服更多是具有长下摆、广袖的样式,这种情况下使用 KawaiiPhysics 又使得布料显得太 Q 弹。
也就是这样,对 KawaiiPhysics 做了一些魔改,在这期间学习到了些关于物理,布料模拟的东西,现记录如下。
Mass-Spring 模型
布料模拟使用了经典的 Mass-Spring 模型,顾名思义,也就是将一块布料当作一张分布有许多质点,且质点间由弹簧互相连接构成的网。
质点
假设模拟的布料是一个均匀分布了 M × N 个质点的矩形,其中的每个质点具有自己的质量、位置以及速度。
弹簧
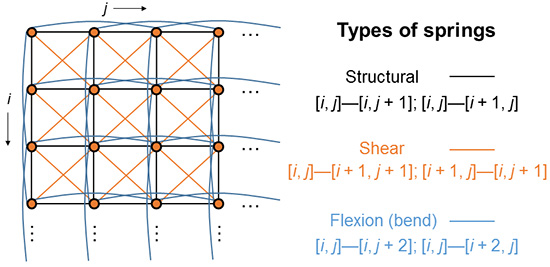
对该系统内的质点,根据质点间连接方式的不同,将材质上每个质点所受到的弹性力分解为以下三种弹簧,对应三种约束(实际上都是距离约束):
- 质点上下左右四个方向相连接的,用于模拟结构约束(Structural)
- 质点斜向对角相连接的,用于模拟剪切约束(Shear)
- 质点上下左右跨一个质点相连接的,用于模拟弯曲约束(Bend)
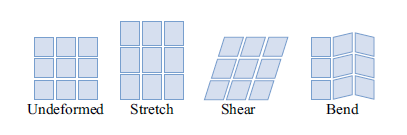
上述三种约束对应到材质上有下面抵抗形变的作用:
- 结构约束用于抵抗布料在垂直方向和水平方向的拉伸,结构约束越强越不易被拉伸
- 剪切约束用于抵抗扭曲,越强就越不会被剪切力所扭曲,更能在质点附近维持原有形状
- 弯曲约束用于抵抗弯曲,越强就不易弯曲,使得材质在视觉上显得质地更硬
参考图 1,将各质点编码,对第 [i,j] 个质点,与他相连的其他的弹簧的位置为:
| 结构约束 | [i, j+1],[i, j-1],[i+1, j],[i-1, j] |
| 剪切约束 | [i+1, j+1],[i+1, j-1],[i-1, j-1],[i-1, j+1] |
| 弯曲约束 | [i, j+2],[i, j-2],[i+2, j],[i-2, j] |
可见对于单个质点而言,它需要周围 12 个质点的信息。
对于弹簧而言还有两个值得注意的变量,刚度(Stiffness)以及原始长度(Rest Length)。
上述的三种约束可以对应各自独立的刚度。对于我们常见的布料材质,通常剪切约束较弱,剪切约束的刚度对材质的视觉效果具有很大影响。此外,结构约束的刚度通常很大,而剪切约束和弯曲约束的刚度都很小1。但这并不意味着这三种约束是相互独立的,比如剪切约束也可以分解为水平方向和垂直方向的约束,可见剪切约束也会一定程度上影响材质的拉伸。
而原始长度 Rest length 用于求解约束,计算某时刻两质点间的相对距离与原始长度 Rest length 的差值,从而确定约束力的大小,其距离约束可以这么表达:
\[\begin{equation} C_{dist}(p_0, p_1) = |p_0-p_1| - d_{rest} \end{equation}\]上述计算弹力并求解约束的过程大致可由代码表达如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void SolveConstraint(Point& P0, Point& P1, const float& Stiffness, const float& RestLength)
{
Vec3 Vector = P1.Position - P0.Position;
float Distance = Vector.Size();
float Force = Stiffness * (Distance - RestLength); // Hooke's Law
Vec3 Displacement = Vector.Normalize() * Force;
float MassSum = P0.Mass + P1.Mass;
float M1Ratio = P1.Mass / MassSum;
P0.Position += Displacement * M1Ratio;
P1.Position -= Displacement * (1.0f - M1Ratio);
}
将质点所受到的弹性力记为 $F_s$,$F_s$ 可和其他外力一同用于计算质点的加速度。
$F_s$ 满足胡克定律,即对弹性系数为 $k_s$ 的材料,有 $F_s = -k_s\, \Delta x$
其他
- 阻尼(Damping)
- 如果没有阻尼的限制,弹簧振子的将会无止境地弹下去,因此引入阻尼来模拟弹簧弹性渐弱,能量流失的过程。对材质阻尼系数为 $c_d$ 速度为 $v$ 的质点,阻尼力 $F_d$ 记为: \(\begin{equation} F_d = -c_d\,v \end{equation}\)
- 重力
- 重力通常作为一个全局常量而存在,不过也不排除部分游戏中有以重力为核心的玩法,在这里我们将重力记为 $F_g$。
- 其他外力
- 至于其他的外力,比较常见的是风力,这些外力可统一记作 $F_e$。
模拟
对基于动力学的模拟方式,大致流程如下:
对于合力 $F$,有
\[\begin{equation} F = F_s + F_d + F_g + F_e \end{equation}\]知道了质点的质量 $m$,根据牛二,可以获得加速度 $a$
\[\begin{equation} a = \frac{F}{m} = \frac{F_s + F_d + F_g + F_e}{m} \end{equation}\]有了加速度便可以根据 $t$ 时刻的速度和位置计算出 $t+1$ 时刻的速度和位置:
\[v_{t+1} = v_t + a\,t\] \[x_{t+1} = x_t + v_{t+1}\,t\]如此迭代,在计算位置和速度时应用上面提到的约束便可以完成基础的模拟逻辑了。
碰撞
由于布料存在于场景中必然会与其他对象发生交互,这就带来了另一个让人抠脑壳的问题,也就是布料与其他对象的碰撞。当严格考虑现实世界的布料时,碰撞将会变得非常复杂,因为还要考虑在布料碰撞的过程中产生的折叠、褶皱等,因此这里暂不深入到这种细节,将着重于对角色-布料和布料-布料这两种碰撞的处理。
布料-角色
对于布料-角色的碰撞,通常的做法是用一系列简单的形状拼合成人形当作角色的代理,但是简单碰撞的形状有限,碰撞凸包的形状会对布料的造型产生影响,弄不好的话会在碰撞代理的连接出产生很难看的葫芦形凹缝。
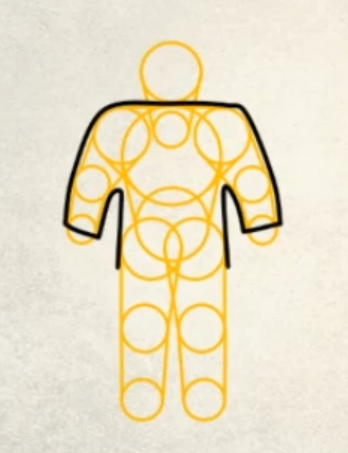
下面对马岛中所使用的人形碰撞:
在对布料进行建模时,在每个质点上会设定一个质点的半径来限制可运动的最大距离。通过参考质点半径以及碰撞的凸包的半径来确定如何校正质点的位置。这个校正过程可以简单的抽象为:检测碰撞→碰撞发生→根据穿深进行反方向校正,大多数布料发生碰撞的过程都遵循这个过程,从而避免穿模。
根据穿深进行校正时有两种解算方式:基于物理和基于位置,区别在于是反方向施加力/冲量,还是施加位移。对于对于模拟的时间步长比较敏感,很容易出现在大时间步时弹出一个巨大的力的问题。因此游戏中布料的碰撞校正通常选择后者,而后者的做法就是 Position Based Dynamic 的思想,不强调施加力的过程,只要能根据最终施加的位移结果能够达成视觉上的正确,那我们就认为它是正确的。
布料-布料
布料-布料碰撞可以分为两种,一种是布料材质与其自身的自碰撞,另一种是使用多层布料时,不同层的布料间的碰撞。
对布料的自碰撞,一个方法是与上次模拟的位置以质点半径做球形的 Sweep 检测来确定,确保质点间的碰撞距离保始终满足 $d_{collision} = min(2r, d_{rest})$,还有限制最大速度等。更多关于布料自碰撞的建议可以参考十分钟物理的这个视频。
对于多层布料的碰撞,可以根据布料质点来构建数个 Quad 然后依据点和三角形的碰撞来处理不同层布料间的碰撞,确保外层布料的点落在内层布料形成的 Quads 外侧。但是这种做法稳定性一般,对于细窄小的飘带有可能会产生很鬼畜的抖动。
或者参考对马岛的方案,将外层布料参考内层布料做蒙皮,为外层布料添加一个值为质点半径的偏移:
这种做法更像是让多层布料分别做球形的碰撞,再让外层布料向内移动一段距离,从而使衣服不会显得太臃肿。
其他补充
时间步长
由于模拟的基础是弹簧,所以不可避免的存在拉伸。对于皮革、绳索这类较硬、并不需要太多拉伸的材质,效果并不是很好。时间步长较短时,会使得材料显得很硬,时间步长较大时,模拟的效果不稳定。
搜集了一番资料,我看到两种比较主流的方法:
一种是尝试使用其他的数值积分方法, 比如 Verlet 积分方法。 Verlet 积分法是在游戏中用得比较多的用于求解牛顿运动方程的数值方法。Verlet 积分方法要解决的问题是,给定 $t$ 时刻的位置 $x$ 和速度 $v$,得到 $t+\Delta t$ 时刻的位置 $x(t+\Delta t)$ 和速度 $v(t+\Delta t)$。简单来说就是,Verlet 积分方法通过将 $v(t)$ 以及 $x(t)$ 做泰勒展开,然后获得新的迭代式:
\[x(t+\Delta t) = 2\,x(t) + x(t-\Delta t) + a(t)\, \Delta t^2\] \[v(t) = \frac{x(t+\Delta t)-x(t-\Delta t)}{2\Delta t}\]具体推导以及误差计算可以参考维基百科。
另一种方法,便是使用 SupStep,即令时间步长划分为多个固定的子步长进行模拟。这个方法会引入额外的计算,但是也加大了模拟的准确度以及稳定性。
我添加了使用 SubStep 的方法,确实稳定性大大提高,但是否使用这种方法还需要根据游戏实际运行状况进行评估。
PBD / XPBD
之前在提到布料-角色碰撞时提到了 PBD(Position Based Dynamic),PBD 是一种基于位置来解碰撞问题的方式,区别于通常基于力的方式。
在 KawaiiPhysics 中操作的单位是骨骼,它是一个基于关节(Joint)的模型,而在它的模型之上使用物理学的方法添加碰撞、约束自然会变得麻烦,因此单纯使用位置来约束碰撞是更合适的方式。
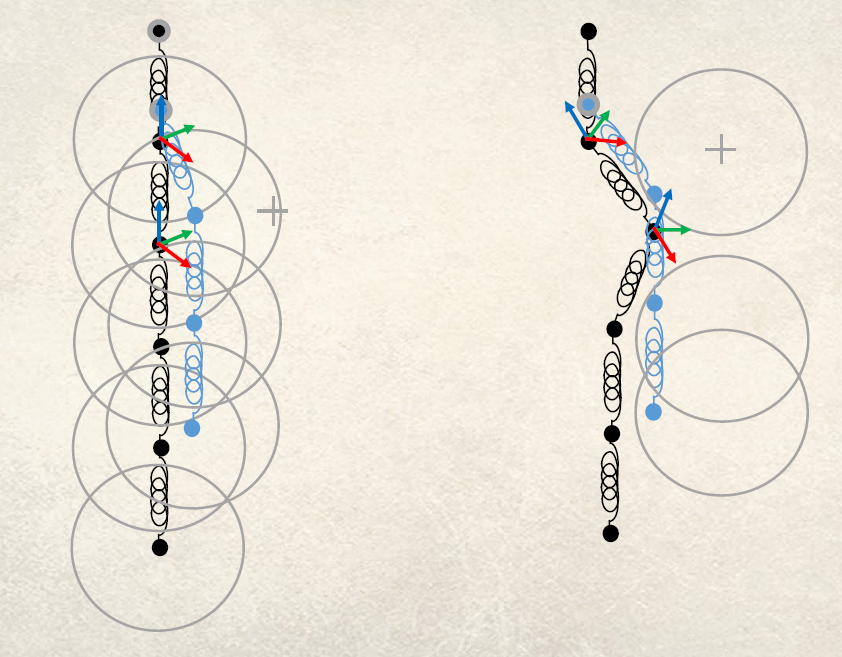
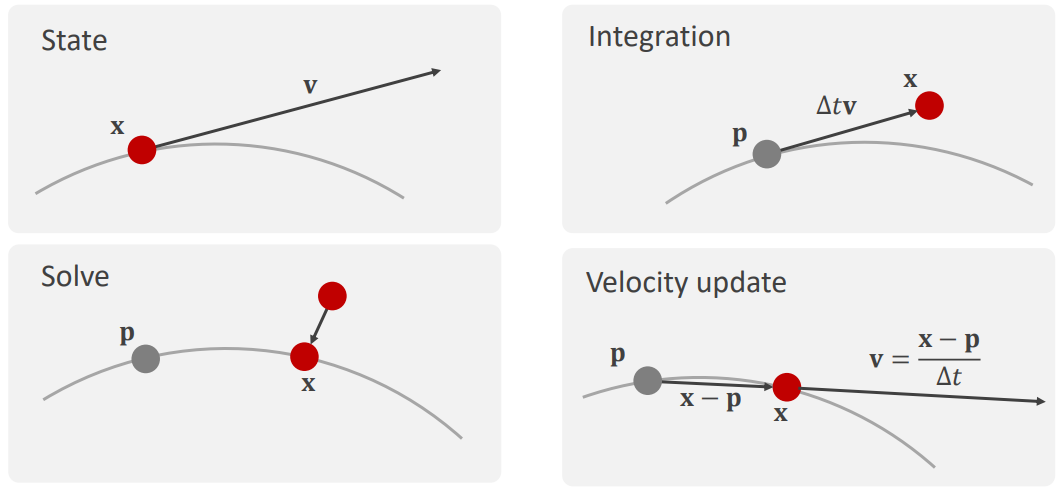
PBD 最大的优势是稳定,发生碰撞时碰撞体不会向外飘。PBD 的核心理念见下图:
根据上一次模拟的速度和时间计算新的位置,然后解算新的位置投影到约束上的点,最后根据投影到约束上点的位置来更新速度。想了解更多的话,这里有中译论文,也可以看原版。还有份更详细的资料在这里。
XPBD 则在 PBD 的基础上解决刚度与迭代次数耦合的问题。关于 XPBD 有一个简单的介绍,作者总结了依据梯度求解约束的通用式子,作者油管频道的其他视频和文章也值得一看,毕竟作者就是这两篇论文的作者。
在对马岛的 GDC talk 中老哥提到一个 “giant hack”,就是对于弹力,完全舍弃掉胡克定律,在每次模拟时使弹簧向原始长度靠拢一点点,我觉得也是利用了 PBD 的思想去做计算。
参考资料
- CS114 Project 3:Cloth Simulation using Mass-Spring System
- Blowing from the West: Simulating Wind in ‘Ghost of Tsushima’
- Cloth Self Collision with Predictive Contacts
- Ten Minute Physics
- Position Based Dynamics
- 游戏模拟——Position based dynamics
(Synthesis Lectures on Visual Computing Computer Graphics, Animation, Computational Photography, and Imaging, #24) Tuur Stuyck_ Brian A. Barsky - Cloth Simulation for Computer Graphics-Morgan & Clayp ↩