DBSCAN 聚类算法

介绍

DBSCAN (Density-based spatial clustering of applications with noise) 是一个基于密度的聚类（Cluster）算法：给定空间里的一个点集，该算法能把附近的点分成一组（有很多相邻点的点），并标记出位于低密度区域的噪声点。

原版论文在这里

概念描述及参数

标识	含义
$D$	样本集
$P_i$	$D$ 中的各样本点
$\epsilon$ (Epsilon)	$P_i$ 的邻域距离阈值
$MinPts$	$P_i$ 在 $\epsilon$ 范围内样本的数量

核心点与边缘点（左）和直接密度可达（右）

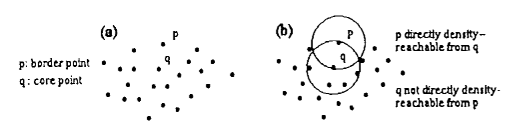
核心点 (Core Points)

满足条件，在 $\epsilon$ 范围内，具有 $MinPts$ 个样本的样本点 $P_i$，称作核心点。

边缘点 (Border Points)

在核心点 $\epsilon$ 范围内，且在样本点 $\epsilon$ 范围内的样本数量小于 $MinPts$，称作边缘点

噪声点 (Noise Points/ Outlier)

非可达点，即不在核心点的 $\epsilon$ 范围内的样本点，称为噪声点

直接密度可达 (directly density-reachable)

当 $P$ 在除 $P$ 以外的任意样本点 $Q$ 的邻域半径 $\epsilon$ 范围内，且 $Q$ 是一个核心点，则称 $P$ 可由 $Q$ 直接（密度）可达。

• 也就是说，核心点 $P$ 的 $\epsilon$ 范围内除 $P$ 以外的点，都是由 $P$ 直接可达的，同理，非核心点没有直接可达的点。

可达性（左）和连接性（右）

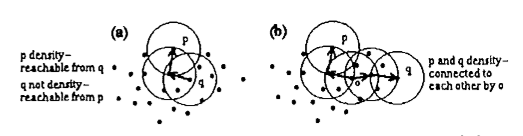
密度可达 (density-reachable)

对于样本中的点，存在路径 $P_1$,…,$P_n$，使 $P_1$ = $P$，$P_n$ = $Q$，如果该路径中任意一点 $P_{i+1}$ 可以由 $P_{i}$ 直接可达，那么称 $Q$ 是可从 $P$ （密度）可达的。

• 根据该定义，非核心点是可以由其他点可达的，但没有点是由非核心点可达的。
• 参考上图，可达性是非对称的，$P$ 到 $Q$ 可达不代表 $Q$ 到 $P$ 可达。

密度相连 (density-connected)

对于样本中的点，存在一个点 $O$ 使得 $P$ 和 $Q$ 都是由 $O$ 可达的，则点 $P$ 和点 $Q$ 被称为（密度）相连的，连接性是对称的。定义了连接性后，每个 Cluster 都符合两个性质：

• 同一个 Cluster 中的任意两点都是相连的。
• 如果 $P$ 是由 Cluster 里的点 $Q$ 可达的，那么 $P$ 和 $Q$ 在同一个 Cluster 中。

举例

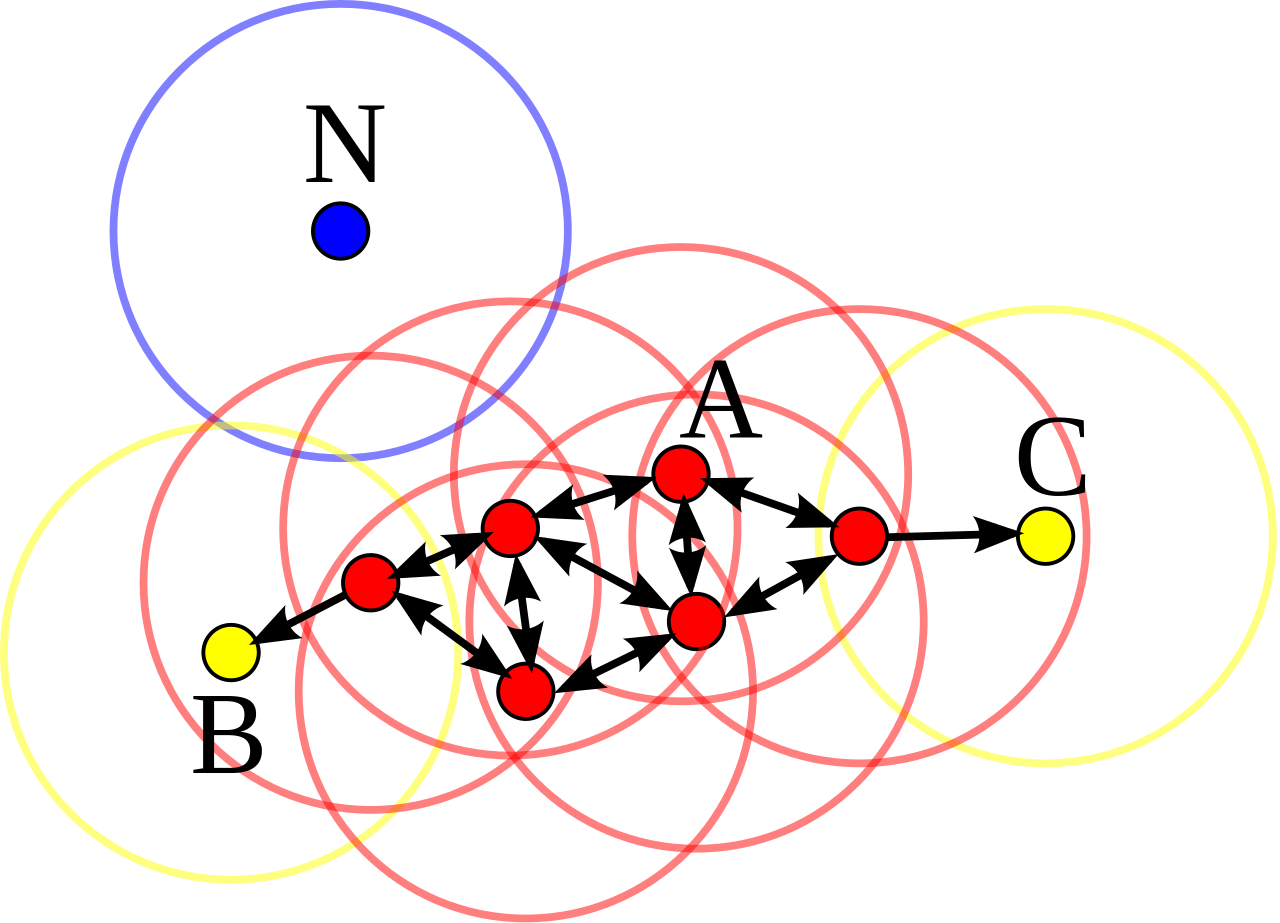
上图中，$MinPts$ = 4，点 A 和其他红色点是核心点，因为它们的 $\epsilon$ 邻域（图中红色圆圈）里包含最少 4 个点（包括自己），由于它们之间相互相可达，它们形成了一个 Cluster。点 B 和点 C 不是核心点，但它们可由 A 经其他核心点可达，作为边缘点加入同一个 Cluster 。点 N 是噪声点，它既不是核心点，又不由其他点可达。

距离函数

这里的距离可以是任意空间内的距离函数，通常使用欧氏距离，在游戏开发中也可能会使用曼哈顿距离。为直观起见，本文中的距离均指的是欧氏距离。

算法

为确定 Cluster, DBSCAN 算法首先从集合里任意一点 $P$ 开始遍历所有密度可达点。然后根据 $\epsilon$ 和 $MinPts$ 判断 $P$ 是核心点还是边缘点。

如果 $P$ 是核心点，该流程会产生一个 Cluster。

如果 $P$ 是边缘点，那么没有任何点是从 $P$ 密度可达的，DBSCAN 将会从样本集中选择下一个点重复该过程。

对于存在多个 Cluster 的情况，算法会根据规则进行合并，这个规则是：

• Cluster 中，对所有 $P$ 的密度可达的点 $Q$ 也属于该 Cluster
• Cluster 中，对所有 $P$ 的密度相连的点 $Q$ 也属于该 Cluster

确定了这些，就明确了 DBSCAN 的算法，简单来说，算法分为下面的步骤：

1. 初始化样本集 $D$，以及 $\epsilon$，$MinPts$
2. 从任意一点 $P$ 开始查询 $\epsilon$ 邻域内的样本点
3. 如果 $\epsilon$ 邻域的点的数量大于等于 $MinPts$，则创建一个 Cluster，否则标记 $P$ 为噪声点（该噪声点也可能位于后续点形成的 Cluster 内）
4. 对除点 $P$ 外满足条件的 $\epsilon$ 邻域内的样本点，逐个查询这些点 $\epsilon$ 邻域内的样本点
5. 如果这些点 $\epsilon$ 邻域的点的数量大于等于 $MinPts$，便将这些点加入此次创建的 Cluster 中
6. 从样本中其他点出发，重复步骤 2 直到遍历完成

论文 4.1 中提供了伪代码：

DBSCAN(SetOfPoints, Eps, MinPts)
// SetOfPoints is UNCLASSIFIED
    ClusterId := nextId(NOISE)
    FOR i FROM 1 TO SetOfPoints.size DO
        Point := SetOfPoints.get(i)
        IF Point.ClId = UNCLASSIFIED THEN
            IF ExpandCluster(SetOfPoints, Point, ClusterId, Eps, MinPts) THEN
                ClusterId := nextId(ClusterId)
            END IF
        END IF
    END FOR
END // DBSCAN

以及创建聚类的 ExpandCluster 函数，经过该函数可以生成一个 Cluster：

ExpandCluster(SetOfPoints, Point, ClId, Eps,MinPts) : Boolean
    //
    // regionQuery 函数用于查询并返回以当前点 Point 为中心的 Eps 邻域中的点
    // seeds 是包含了从点 Point 出发的所有可达点的集合
    // 
    seeds := SetOfPoints.regionQuery(Point, Eps)
    IF seeds.size < MinPts THEN // no core point
        //
        // 对 Eps 邻域内的样本数量不足 MinPts 个的非核心点（边缘点），由于非核心点没有可达点，因此返回 false。
        // 这里虽然标记为 NOISE 但在后续步骤可能会改变该标记
        //
        SetOfPoint.changeClId(Point, NOISE)
        RETURN False
    ELSE // all points in seeds are density-reachable from Point
        //
        // 这里的点是除了初始点 Point 外所有满足 MinPts 和 Eps 的直接密度可达的点，
        // 因此先将这些点加入同一个 Cluster 中，并将初始点 Point 删除
        //
        SetOfpoints.changeClId(seeds, ClId)
        seeds.delete(Point)
        WHILE seeds <> Empty DO
            currentP := seeds.first()
            //
            // 从该 Cluster 中的其他点出发，查找其他的 Eps 邻域内可达的点
            //
            result := SetOfpoints.regionQuery(currentP, Eps)
            IF result.size >= MinPts THEN
                FOR i FROM 1 TO result.size DO
                    resultP := result.get(i)
                    //
                    // 如果可达点暂未划分到其他 Cluster 中（包括此前被标记为 NOISE 的），便将该点加入到该 Cluster 中
                    // 若此前未归类过，便将该可达点加入可达点的集合 seeds 中
                    //
                    IF resultP.ClId IN {UNCLASSIFIED, NOISE} THEN
                        IF resultP.ClId = UNCLASSIFIED THEN
                            seeds.append(resultP)
                        END IF
                        SetOfPoints.changeClId(resultP, ClId)
                    END IF // UNCLASSIFIED or NOISE
                END FOR
            END IF // result.size >= MinPts
            //
            // 查询完成后从将当前点从点集中删除
            //
            seeds.delete(currentP)
        END WHILE // seeds <> Empty
        RETURN True
    END IF
END // ExpandCluster

评估

参数

参数的选择向来是个令人头大的问题，在对样本集缺少了解的情况下，很难选出合适的参数。论文中提到了一种叫做 k-distance 的选择 $\epsilon$ 的方法，我将在应用时加以解释。但是即使如此，这个过程也是要不断迭代，最好在数据可视化时进行调整。

假如样本集中的点密度差异较大，也很难产生一个满足所有情况的聚类结果，因为全局的参数 $\epsilon$ 和 $MinPts$ 只有一套。密度变化较大的情况，可以考虑使用 OPTICS 或者 HDBSCAN。

稳定性

DBSCAN 的结果是确定的，对于给定顺序的数据集来说，相同参数下生成的 Clusters 是相同的。然而，当相同数据的顺序不同时，生成的 Clusters 较之另一种顺序会有所不同。

首先，即使不同顺序的数据集的核心点是相同的，Clusters 的标签会取决于数据集中各采样点的顺序。其次，可达点被分配到哪个 Clusters 也是会受到数据顺序的影响的，比如一个边缘采样点位于一个分属于两个不同的 Clusters 的核心点的 $\epsilon$ 邻域内，这时该边缘点被分配到哪个 Cluster 中取决于哪一个 Cluster 先创建。

因此说 DBSCAN 是不稳定的。

效率

算法中遍历了所有的样本点，但实践中算法的时间消耗往往受到 regionQuery 函数的制约。

对于 regionQuery 函数，论文中提到可以使用 R* 树来创建空间索引以提高效率，实践中也可以使用其他的空间划分方法，比如 kd 树。算法期望 $\epsilon$ 邻域范围内的点的数量比起整个样本集的数量是一个较小的值，因此每次查询的时间复杂度为 O(logn)。由于对列表中的每个点的都要进行一次 regionQuery，因此 DBSCAN 的平均的时间复杂度为 O(n * logn)。

当 $\epsilon$ 较大，且 $D$ 数量也比较庞大时，regionQuery 建树的时间消耗会非常大。

参考

• DBSCAN
• scikit-leran clustering
• 基于密度的聚类算法（1）——DBSCAN详解
• 常用聚类算法
• DBSCAN Clustering Easily Explained with Implementation