首页 Filament 材质篇（上）
文章
取消

Filament 材质篇（上）

发表于 2019/06/29
作者 Yohiro
28 分钟阅读

本篇是 Filament 的笔记，以及部分自己的理解。

可以结合 Desktop 的渲染方式一起，看 Filament 的渲染为了更好地支持移动端，舍弃了哪些。

也可以搭配 【GAMES101-现代计算机图形学入门-闫令琪】 食用，风味更佳。

原则

Filament 是用于 Android 的渲染引擎，设计原则包含以下几个方面：

  • 性能，关注实时渲染中移动设备的性能表现，主要目标为 OpenGL ES3.x 版本的 GPU
  • 质量，同时兼顾中低性能的 GPU
  • 易用，方便美术同学直观且快速地迭代资产，因此提供易理解地参数以及物理上合理的视觉效果
  • 熟悉，该系统应尽可能使用物理单位，如以开尔文为单位地色温、以流明为单位的光照等
  • 灵活，支持非真实感渲染

PBR

选择采用 PBR 是因为它从艺术和生产效率的角度来看有好处，而且它能很好的兼容设计目标。

与传统模型相比，PBR 是一种可以更准确地表示材质及其与光的交互方式的方法。PBR 方法的核心是材质和光照的分离，可以创建在统一光照条件下看起来可信的资产。

概念

符号定义
$v$观察视角的单位向量
$l$入射光线的单位向量
$n$表面法线的单位向量
$h$单位半角向量
$f$BRDF
$f_d$BRDF 的漫反射项
$f_r$BRDF 的镜面反射项
$\alpha$粗糙度
$\sigma$漫反射率
$\Omega$球体区域
$f_0$入射法向的反射率
$f_{90}$掠射角的反射率
$\chi^+(a)$阶跃函数（a>0 则为 1，否则为 0）
$n_{ior}$界面折射率（IOR，Index of refraction）
$\left< n \cdot l \right>$[0, 1] 的点积
$\left< a \right>$[0, 1] 的值

材质系统

详见👉Filament 材质指南 以及 材质属性

标准模型

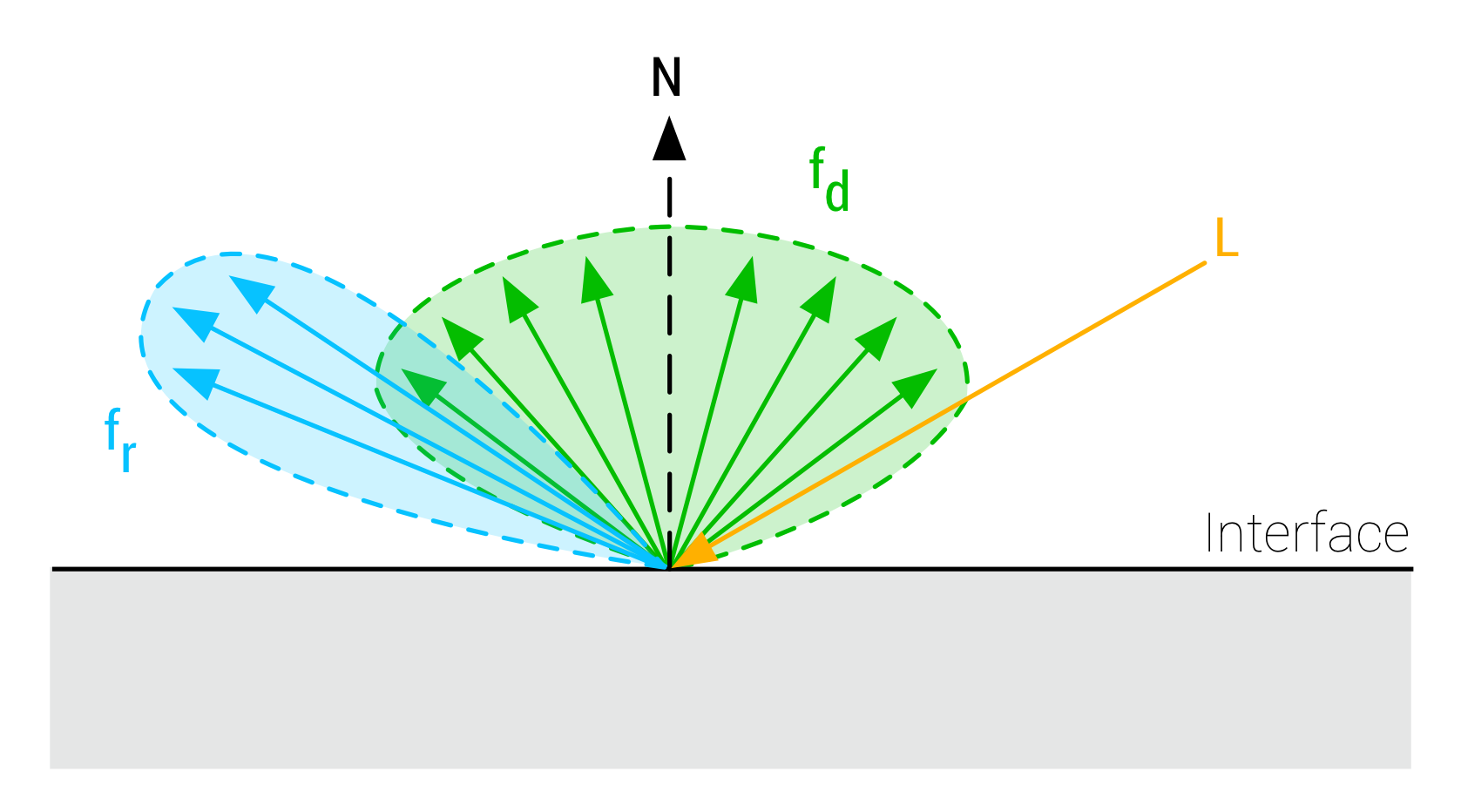
标准的材质模型通过 BSDF（双向散射分布函数）来表达，BSDF 有两个组成部分 BRDF（双向反射分布函数）以及 BTDF（双向透射函数）。 由于绝大多数材质对表面材质进行模拟，因而具有各项同性的标准材质模型会专注于 BRDF，从而忽略或近似 BTDF。

BRDF 将标准材质的表面分为：

  • 漫反射项 $f_d$
  • 镜面反射项 $f_r$

fr_fd BRDF 模型中的$f_d$和$f_r$

完整的表达为：

\[f(v,l)=f_d(v,l)+f_r(v,l)\]

上述方程描述的是单一入射光，完整的渲染方程中将会对整个半球面上的入射光线 $l$ 进行积分。

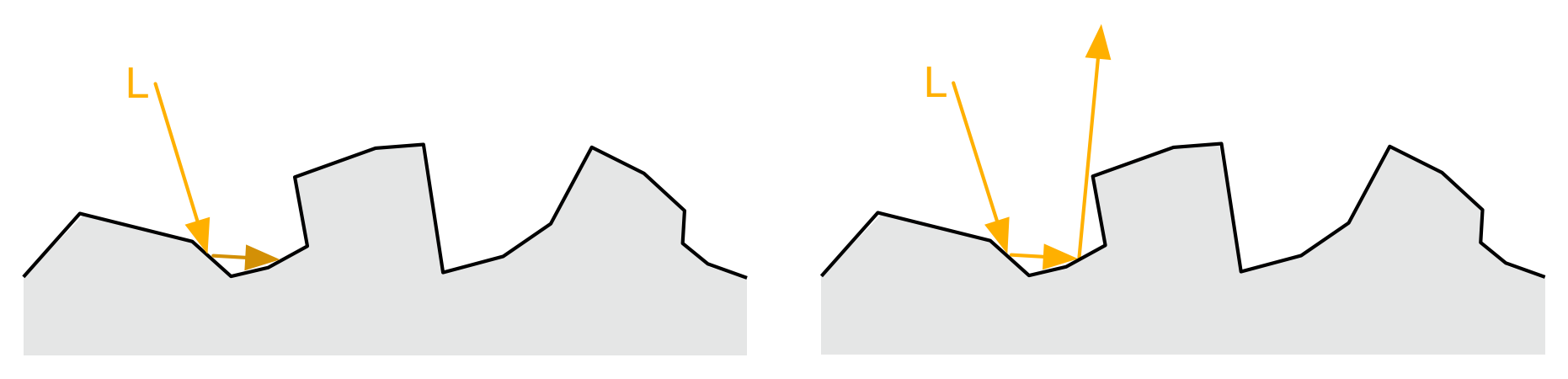
通常，材质表面并非是完全光滑的，因此引入了微表面模型/微表面 BRDF 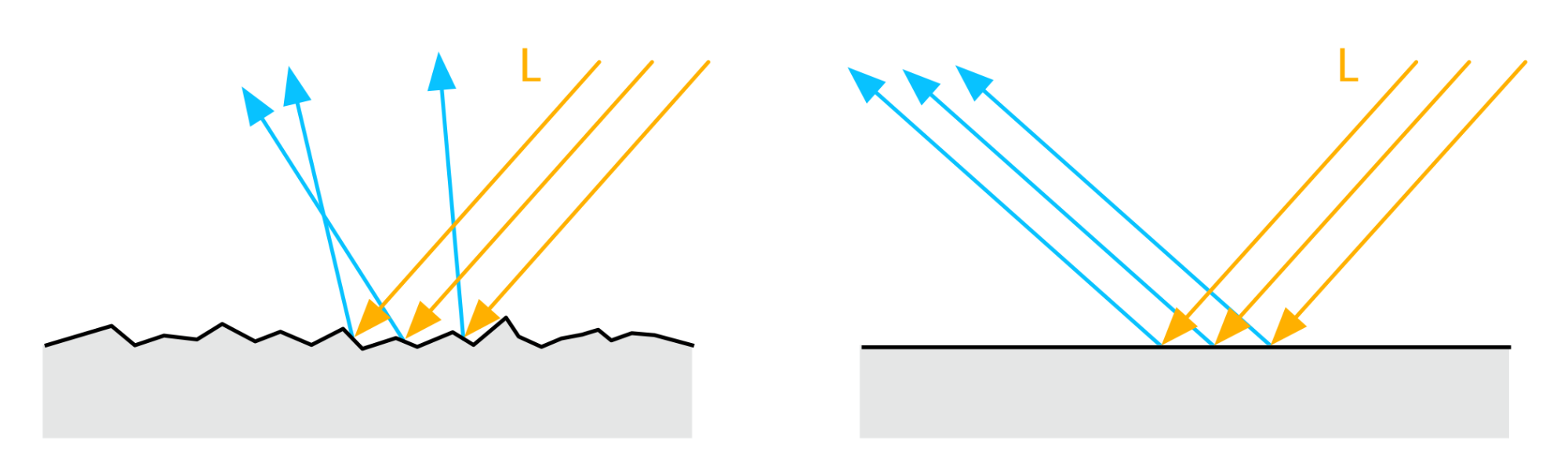microfacet 微表面模型的粗糙表面和光滑表面

在微表面，法线 N 位于入射光和观察方向之间的半角方向时会反射可见光。 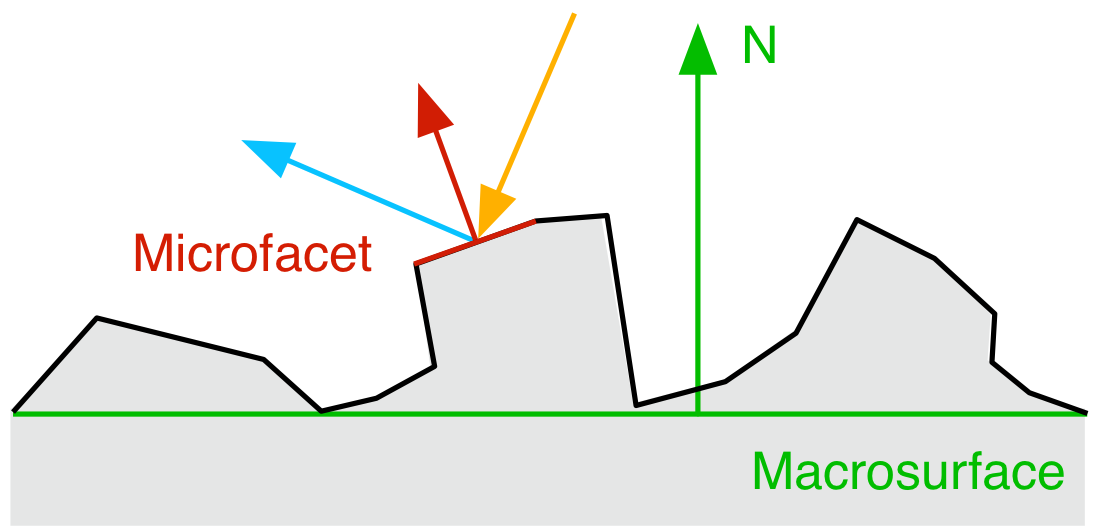microsurface

但是也并非所有符合上面条件的法线会贡献反射，因为微表面 BRDF 会考虑材质表面的遮蔽而产生的自阴影。 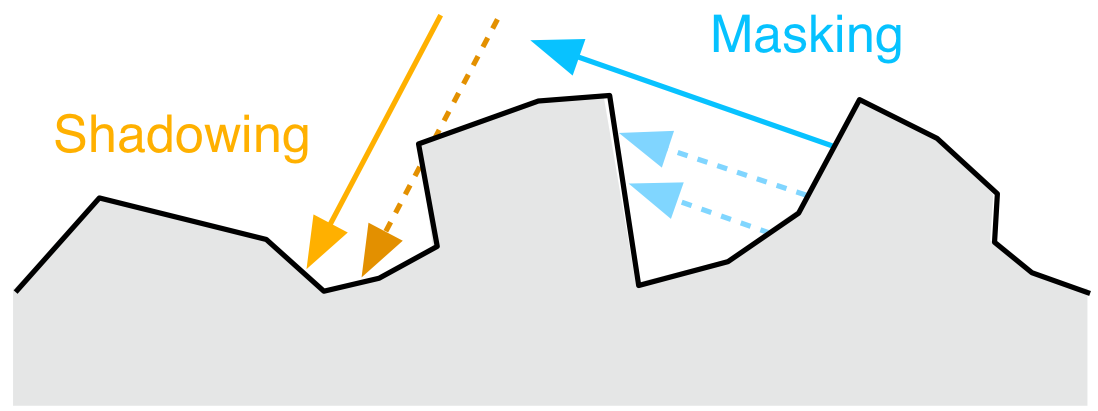shadow masking

粗糙度高的材质，表面朝向相机的面越少，表现为越模糊，因为入射光的能量被分散了。 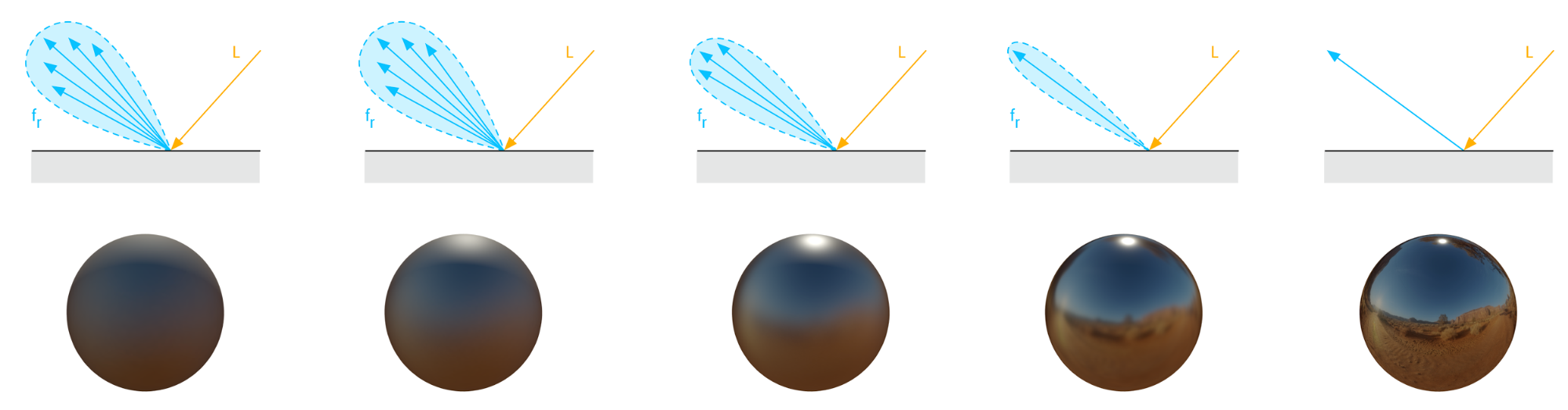roughness 光照对不同粗糙度的影响，从左到右表面逐渐光滑

下面的方程描述了微表面模型：

\[\begin{equation} f_x(v,l) = \frac{1}{|n \cdot v| |n \cdot l|} \int_\Omega D(m,\alpha) G(v,l,m) f_m(v,l,m) (v \cdot m) (l \cdot m) dm \end{equation}\]

其中 D 项描述微表面的法线分布，G 项对微表面的几何性质（主要是阴影和遮蔽）进行描述。主要的不同来自于对半球微表面的积分$f_m$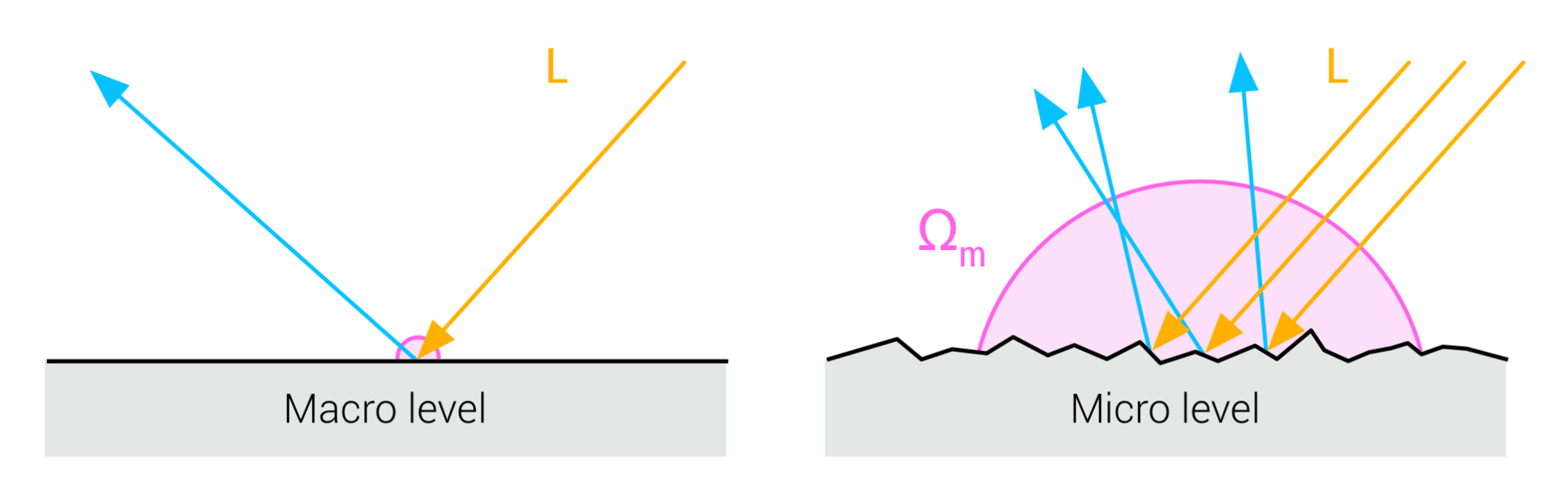： 宏观层面的平面（左）和微观层面的微表面（右） 在微观层面上，材质的表面并非完全平坦，就无法再假设所有的入射光是平行的，因此需要对半球进行积分，但对半球的完整的积分在实时渲染中不切实际，因此需要采用近似值。

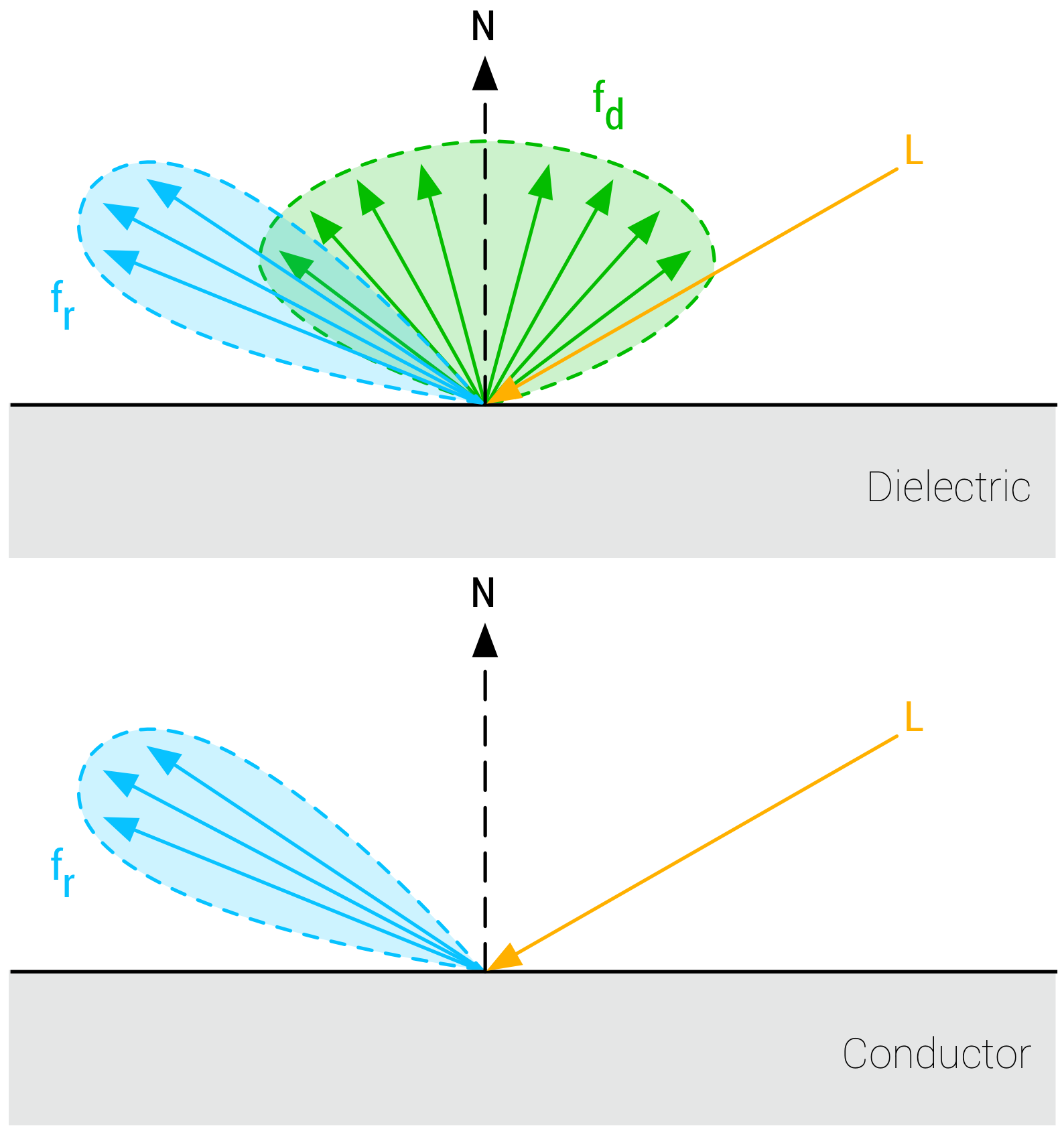
电介质和导体

Filament 里对材质属性引入了两个概念：电介质和导体。

入射光照射到 BRDF 模拟的材质表面后，光被分解为漫反射和镜面反射两个分量，这是一种简化的模型。

实际上，会有入射光穿透表面，在材质内部进行散射，最后再以漫反射的形式离开表面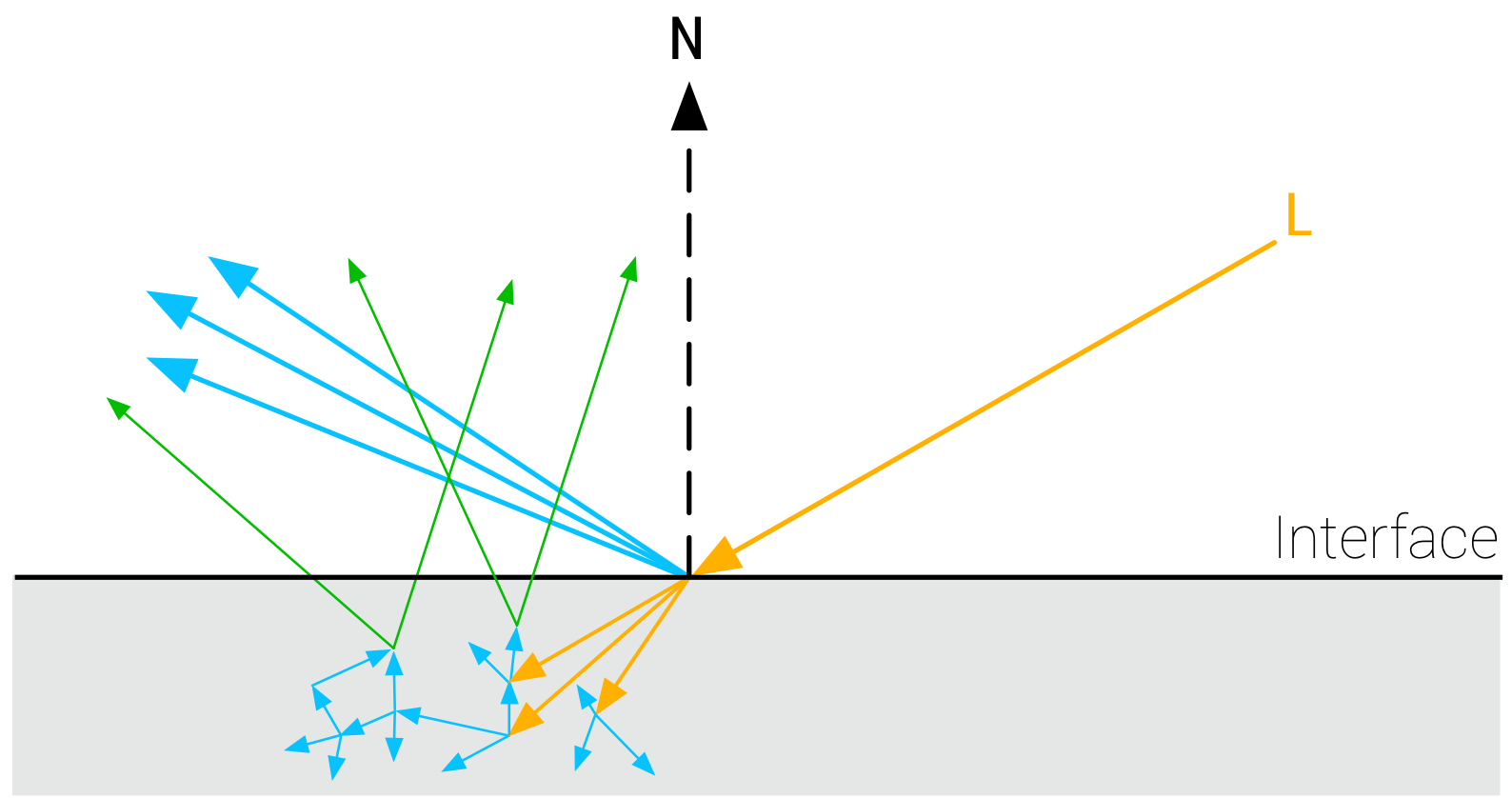： 漫反射的散射

这就是电介质和导体的区别。导体不会产生次表面散射，散射发生在电介质当中。

电介质和导体表面的 BRDF 模型

Specular BRDF

在 Cook-Torrance 的微表面模型中，Specular BRDF 可描述为，

\[\begin{equation} f_r(v,l) = \frac{D(h, \alpha) G(v, l, \alpha) F(v, h, f0)}{4 (n \cdot v)(n \cdot l)} \end{equation}\]

在实时渲染领域常采用对 D、G、F 项的近似，这里 提供了更多关于 Specular BRDF 的参考。

D 正态分布函数 (Normal Distribution Function)

正态分布函数（NDF）是描述现实世界物体表面分布的一种方式，但在实时渲染领域常用的是 Walter 描述的 GGX 分布，GGX 具有长衰减和短峰值的特点，GGX 的分布函数如下：

\[\begin{equation} D_{GGX}(h,\alpha) = \frac{\alpha^2}{\pi ( (n \cdot h)^2 (\alpha^2 - 1) + 1)^2} \end{equation}\]

下面是来自 UnrealEngine 中的实现，其中 a2 是$\alpha^2$

1
2
3
4
5
6
7

// GGX / Trowbridge-Reitz
// [Walter et al. 2007, "Microfacet models for refraction through rough surfaces"]
float D_GGX( float a2, float NoH )
{
    float d = ( NoH * a2 - NoH ) * NoH + 1; // 2 mad
    return a2 / ( PI*d*d );             // 4 mul, 1 rcp
}

一个常见的优化手段是使用半精度的浮点数，即half类型进行计算。因为公式展开中的 $1-(n \cdot h)^2$ 项存在精度问题：

  • 高光情况下，即当 $(n \cdot h)^2$ 接近 1 时，该项会因为浮点数的差值计算问题被截断，导致结果为零。
  • $n \cdot h$本身在接近 1 时缺少足够的精度。

为避免精度造成的问题，可以用叉积的展开式代换，

\[\begin{equation} | a \times b |^2 = |a|^2 |b|^2 - (a \cdot b)^2 \end{equation}\]

由于 $n$ 和 $l$ 是单位向量，便有

\[\begin{equation} |n \times h|^2 = 1 - (n \cdot h)^2 \end{equation}\]

这样一来，我们便可以直接使用叉积来直接计算 $1-(n \cdot h)^2$

Filament 中的实现如下

1
2
3
4
5
6
7
8
9
10

#define MEDIUMP_FLT_MAX    65504.0
#define saturateMediump(x) min(x, MEDIUMP_FLT_MAX)

float D_GGX(float roughness, float NoH, const vec3 n, const vec3 h) {
    vec3 NxH = cross(n, h);
    float a = NoH * roughness;
    float k = roughness / (dot(NxH, NxH) + a * a);
    float d = k * k * (1.0 / PI);
    return saturateMediump(d);
}

G 几何阴影（Geometric Shadowing）

根据 Heitz 2014, “Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs”1，Filament 使用的 Smith 几何阴影公式如下：

\[\begin{equation} G(v,l,\alpha) = G_1(l,\alpha) G_1(v,\alpha) \end{equation}\]

其中 $G_1$ 可使用多种模型，实时渲染中常使用 GGX 公式，

\[\begin{equation} G_1(v,\alpha) = G_{GGX}(v,\alpha) = \frac{2 (n \cdot v)}{n \cdot v + \sqrt{\alpha^2 + (1 - \alpha^2) (n \cdot v)^2}} \end{equation}\]

完整版即为，

\[\begin{equation} G(v,l,\alpha) = \frac{2 (n \cdot l)}{n \cdot l + \sqrt{\alpha^2 + (1 - \alpha^2) (n \cdot l)^2}} \frac{2 (n \cdot v)}{n \cdot v + \sqrt{\alpha^2 + (1 - \alpha^2) (n \cdot v)^2}} \end{equation}\]

注意到 $G(v,l,\alpha)$ 的分子为 $4(n \cdot l) (n \cdot v)$ 这里再贴一次我们所使用的 specular BRDF，

\[\begin{equation} f_r(v,l) = \frac{D(h, \alpha) G(v, l, \alpha) F(v, h, f0)}{4 (n \cdot v)(n \cdot l)} \end{equation}\]

通过引入可见性函数 Visibility 项 $V(v,l,\alpha)$，将 $f_r$ 变为：

\[\begin{equation} f_r(v,l) = D(h, \alpha) V(v, l, \alpha) F(v, h, f_0) \end{equation}\]

其中

\[\begin{equation} V(v,l,\alpha) = \frac{G(v, l, \alpha)}{4 (n \cdot v) (n \cdot l)} = V_1(l,\alpha) V_1(v,\alpha) \end{equation}\]

便可消去分子，得到

\[\begin{equation} V_1(v,\alpha) = \frac{1}{n \cdot v + \sqrt{\alpha^2 + (1 - \alpha^2) (n \cdot v)^2}} \end{equation}\]

论文指出，通过引入微表面的高度来建模可以得到更好的结果。引入了高度$h$的 Smith 函数：

\[\begin{equation} G(v,l,h,\alpha) = \frac{\chi^+(v \cdot h) \chi^+(l \cdot h)}{1 + \Lambda(v) + \Lambda(l)} \end{equation}\] \[\begin{equation} \Lambda(m) = \frac{-1 + \sqrt{1 + \alpha^2 tan^2(\theta_m)}}{2} = \frac{-1 + \sqrt{1 + \alpha^2 \frac{(1 - cos^2(\theta_m))}{cos^2(\theta_m)}}}{2} \end{equation}\]

其中$\theta_m$是镜面法线$n$与观察方向$v$的夹角，因此有$cos(\theta_m) = n \cdot v$，代换后得到

\[\begin{equation} \Lambda(v) = \frac{1}{2} \left( \frac{\sqrt{\alpha^2 + (1 - \alpha^2)(n \cdot v)^2}}{n \cdot v} - 1 \right) \end{equation}\]

由此得出可见性函数，

\[\begin{equation} V(v,l,\alpha) = \frac{0.5}{n \cdot l \sqrt{(n \cdot v)^2 (1 - \alpha^2) + \alpha^2} + n \cdot v \sqrt{(n \cdot l)^2 (1 - \alpha^2) + \alpha^2}} \end{equation}\]

Unreal 中的实现如下：

1
2
3
4
5
6
7

// [Heitz 2014, "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs"]
float Vis_SmithJoint(float a2, float NoV, float NoL) 
{
    float Vis_SmithV = NoL * sqrt(NoV * (NoV - NoV * a2) + a2);
    float Vis_SmithL = NoV * sqrt(NoL * (NoL - NoL * a2) + a2);
    return 0.5 * rcp(Vis_SmithV + Vis_SmithL);
}

考虑到根号下都是平方项，且每项∈[0,1]，于是可优化为：

\[\begin{equation} V(v,l,\alpha) = \frac{0.5}{n \cdot l (n \cdot v (1 - \alpha) + \alpha) + n \cdot v (n \cdot l (1 - \alpha) + \alpha)} \end{equation}\]

虽然在数学上是错的，但对于移动设备的实时渲染是足够的。Filament 中的实现如下：

1
2
3
4
5
6

float V_SmithGGXCorrelatedFast(float NoV, float NoL, float roughness) {
    float a = roughness;
    float GGXV = NoL * (NoV * (1.0 - a) + a);
    float GGXL = NoV * (NoL * (1.0 - a) + a);
    return 0.5 / (GGXV + GGXL);
}

[Hammon17] 提出了相似的优化思路，通过插值来实现：

\[\begin{equation} V(v,l,\alpha) = \frac{0.5}{lerp(2 (n \cdot l) (n \cdot v), (n \cdot l) + (n \cdot v), \alpha)} \end{equation}\]

F 菲涅尔（Fresnel）

菲涅尔项定义了光在两种不同介质的交界处如何处理反射和折射，或者说反射的能量与透射的能量的比率。

反射光的强度不仅取决于视角，还取决于材质的折射率 IOR。将入射光线垂直于表面时（Normal）反射率记为$f_0$，掠射角（Grazing）反射率记为$f_{90}$。根据 [Schlick94] 描述，在 Cook-Torrance 的微表面模型中，Specular BRDF 的菲涅尔项的一种近似可写为：

\[\begin{equation} F_{Schlick}(v,h,f_0,f_{90}) = f_0 + (f_{90} - f_0)(1 - v \cdot h)^5 \end{equation}\]

Unreal 的实现如下：

1
2
3
4
5

float3 F_Schlick(float3 F0, float3 F90, float VoH)
{
    float Fc = Pow5(1 - VoH);
    return F90 * Fc + (1 - Fc) * F0;
}

该菲涅尔函数可当作入射反射率和掠射角反射率间的插值，可以取$f_{90}$为 1.0 来达到近似。

Diffuse BRDF

漫反射中常用 Lambertian 函数，漫反射的 BRDF：

\[\begin{equation} f_d(v,l) = \frac{\sigma}{\pi} \frac{1}{| n \cdot v | | n \cdot l |} \int_\Omega D(m,\alpha) G(v,l,m) (v \cdot m) (l \cdot m) dm \end{equation}\]

Filament 中的实现，假定微表面半球面产生均一的漫反射，因此一个简单的 Lambertian BRDF 为

\[\begin{equation} f_d(v,l) = \frac{\sigma}{\pi} \end{equation}\]

实现也非常简单，

1
2
3
4
5

float Fd_Lambert() {
    return 1.0 / PI;
}

vec3 Fd = diffuseColor * Fd_Lambert();

迪士尼的 BRDF 和 Oren-Nayar 模型都考虑到了粗糙度的影响，并会在掠射角出产生细微的逆反射。迪士尼的 Diffuse BRDF 如下：

\[\begin{equation} f_d(v,l) = \frac{\sigma}{\pi} F_{Schlick}(n,l,1, f_{90}) F_{Schlick}(n,v,1,f_{90}) \end{equation}\]

其中

\[\begin{equation} f_{90}=0.5 + 2 \cdot \alpha cos^2(\theta_d) \end{equation}\]

Unreal 中对这两种模型的 Diffuse BRDF 的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

// [Burley 2012, "Physically-Based Shading at Disney"]
float3 Diffuse_Burley( float3 DiffuseColor, float Roughness, float NoV, float NoL, float VoH )
{
    float FD90 = 0.5 + 2 * VoH * VoH * Roughness;
    float FdV = 1 + (FD90 - 1) * Pow5( 1 - NoV );
    float FdL = 1 + (FD90 - 1) * Pow5( 1 - NoL );
    return DiffuseColor * ( (1 / PI) * FdV * FdL );
}

// [Gotanda 2012, "Beyond a Simple Physically Based Blinn-Phong Model in Real-Time"]
float3 Diffuse_OrenNayar( float3 DiffuseColor, float Roughness, float NoV, float NoL, float VoH )
{
    float a = Roughness * Roughness;
    float s = a;// / ( 1.29 + 0.5 * a );
    float s2 = s * s;
    float VoL = 2 * VoH * VoH - 1;      // double angle identity
    float Cosri = VoL - NoV * NoL;
    float C1 = 1 - 0.5 * s2 / (s2 + 0.33);
    float C2 = 0.45 * s2 / (s2 + 0.09) * Cosri * ( Cosri >= 0 ? rcp( max( NoL, NoV ) ) : 1 );
    return DiffuseColor / PI * ( C1 + C2 ) * ( 1 + Roughness * 0.5 );
}

Lambertian diffuse BRDF 和 Disney diffuse BRDF 的效果对比。从最左侧边缘可以看出，Disney 的模型在掠射角有细微的不同。

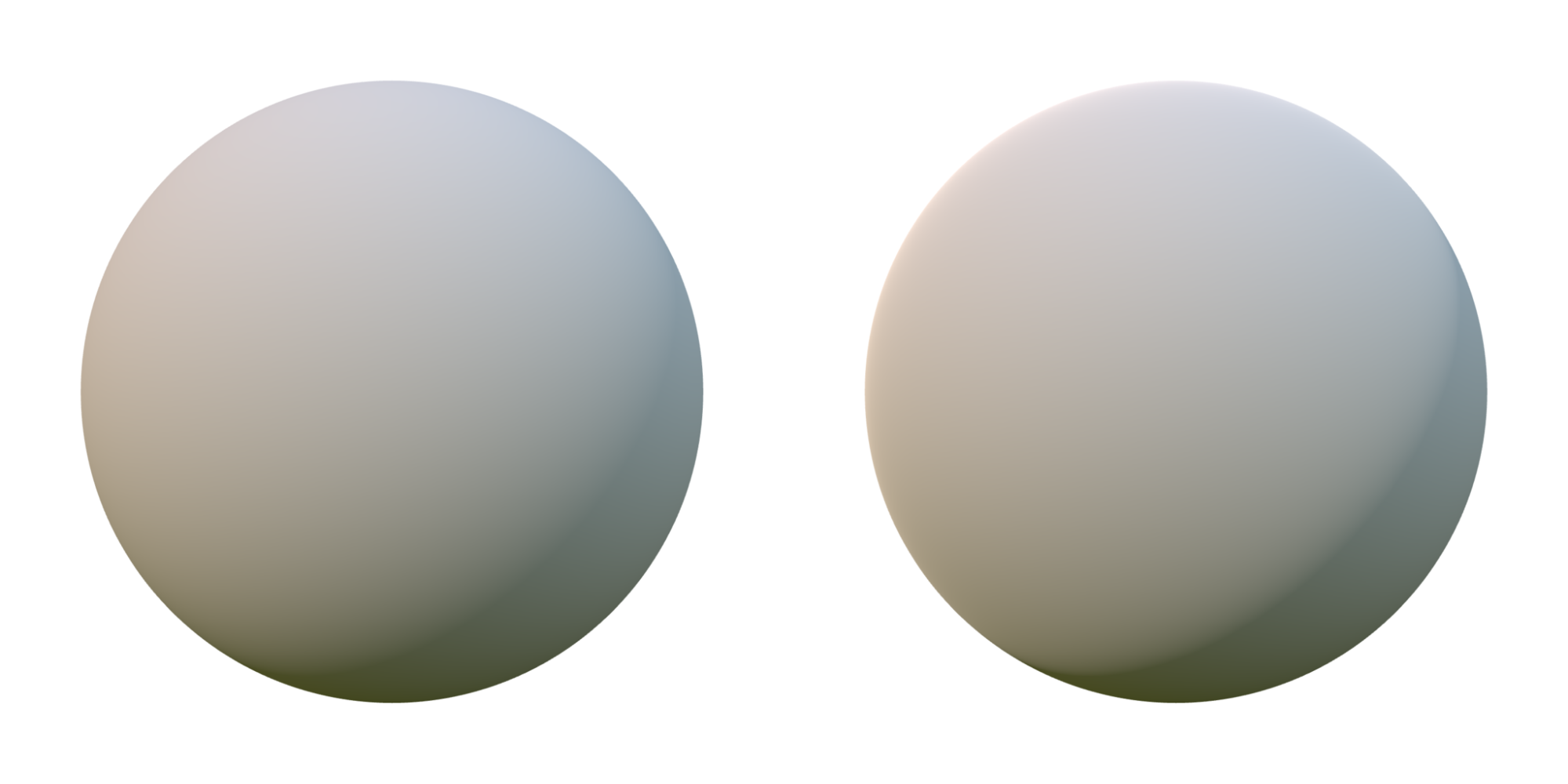Lambertian diffuse BRDF（左）和 Disney diffuse BRDF（右）

标准模型总结

镜面反射项
Cook-Torrance 镜面反射微表面模型/GGX 正态分布函数/Smith-GGX 高度相关可见性函数/Schlick Fresnel 函数
漫反射项
Lambert 漫反射模型

标准模型的 GLSL 实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

float D_GGX(float NoH, float a) {
    float a2 = a * a;
    float f = (NoH * a2 - NoH) * NoH + 1.0;
    return a2 / (PI * f * f);
}

vec3 F_Schlick(float u, vec3 f0) {
    return f0 + (vec3(1.0) - f0) * pow(1.0 - u, 5.0);
}

float V_SmithGGXCorrelated(float NoV, float NoL, float a) {
    float a2 = a * a;
    float GGXL = NoV * sqrt((-NoL * a2 + NoL) * NoL + a2);
    float GGXV = NoL * sqrt((-NoV * a2 + NoV) * NoV + a2);
    return 0.5 / (GGXV + GGXL);
}

float Fd_Lambert() {
    return 1.0 / PI;
}

void BRDF(...) {
    vec3 h = normalize(v + l);

    float NoV = abs(dot(n, v)) + 1e-5;
    float NoL = clamp(dot(n, l), 0.0, 1.0);
    float NoH = clamp(dot(n, h), 0.0, 1.0);
    float LoH = clamp(dot(l, h), 0.0, 1.0);

    // perceptually linear roughness to roughness (see parameterization)
    float roughness = perceptualRoughness * perceptualRoughness;

    float D = D_GGX(NoH, a);
    vec3  F = F_Schlick(LoH, f0);
    float V = V_SmithGGXCorrelated(NoV, NoL, roughness);

    // specular BRDF
    vec3 Fr = (D * V) * F;

    // diffuse BRDF
    vec3 Fd = diffuseColor * Fd_Lambert();

    // apply lighting...
}

提升 BRDF

一个好的 BRDF 函数是能量守恒的，上述探讨的 BRDF 存在两个问题。

漫反射获取的能量
Lambert 模型的 Diffuse BRDF 没有考虑表面反射的光
镜面反射损失的能量
Cook-Torrance BRDF 在微表面上建模，但考虑的是单次光的反射，这种近似使得高粗糙度下存在能量损失，导致其表面的能量不守恒。

单次反射光与多重散射

基于此，可以说，表面越粗糙，产生的多重散射越多，从而能量损失的越多。这种能量的损失带来的结果便是材质会变暗，金属表面更易受到这种影响，因为金属材质的反射都是镜面反射，参见下图的对比： 仅考虑了单次散射的金属材质

考虑了多重散射的金属材质

参数

迪士尼的材质模型2 包含* baseColor、subsurface、metallic、specular、specularTint、roughness、anisotropic、sheen、sheenTint、clearcoat、clearcoatGloss *共 11 项，考虑到实时渲染的性能要求以及方便美术同学和开发同学使用，因此，Filament 使用了简化模型。

参数定义
BaseColor非金属材质表面的漫反射反照率和金属材质表面的镜面颜色
Metallic表面是电介质（0.0）或导体（1.0）
Roughness表面的粗糙度
Reflectance电介质表面法向入射$f_0$时的菲涅耳反射率
Emissive模拟自发光表面额外的漫反射反照率，常见于具有泛光效果的 HDR 管线中
Ambient Occlusion定义材质表面某点半球面上接收的环境光量，是每像素阴影系数

从上到下：不同的金属度、不同电介质粗糙度、不同的金属粗糙度、不同的反射率

参数类型和范围
BaseColor[0,1] 的 Linear RGB
Metallic[0,1] 的标量
Roughness[0,1] 的标量
Reflectance[0,1] 的标量
Emissive[0,1] 的 Linear RGB + 曝光补偿
Ambient Occlusion[0,1] 的标量

上述的类型以及范围是对 Shader 而言的，在参数到达 Shader 之前可以用 sRGB 表示，在传入 Shader 前转换到 linear space 即可。

重映射

为了使美术同学更直观地使用标准材质模型，因此引入了对 baseColor, roughness, reflectance 的重映射。

BaseColor

材质的 baseColor 会受其金属程度影响。电介质材质具有单一颜色的镜面反射，但会保留 baseColor 作为漫反射颜色。而导体材质使用 baseColor 作为镜面反射的颜色，没有漫反射。

因此，对于漫反射的颜色，有以下转换：

1

vec3 diffuseColor = (1.0 - metallic) * baseColor.rgb;

Roughness

在 Filament 中，使用者所指定的粗糙度叫做perceptualRoughness 感知粗糙度，是一种直观的、经验性的值，这种粗糙度会使用下面公式映射到线性空间，

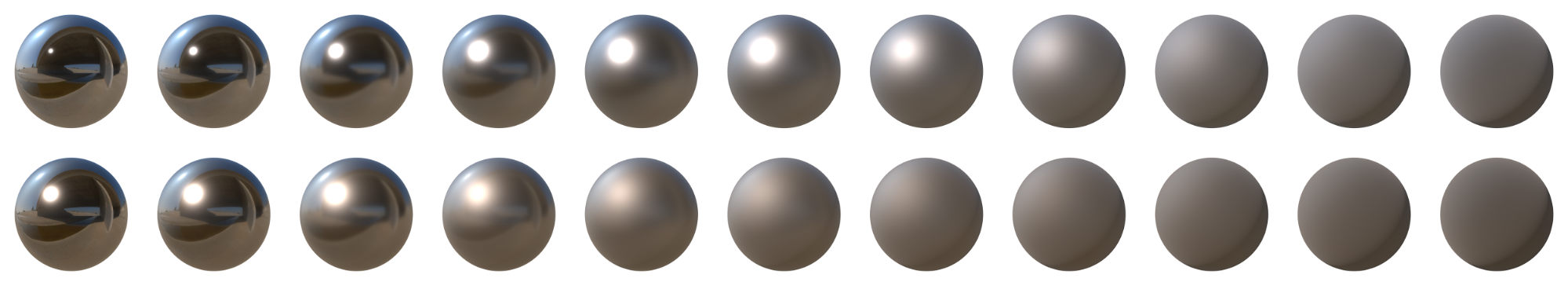\[\begin{equation} \alpha = perceptualRoughness^2 \end{equation}\]

感知线性粗糙度 (PerceptualRoughness，上）和重映射的粗糙度（$\alpha$，下）

可见，重映射的粗糙度更方便美术同学理解。若不经重映射，光滑金属表面的值必须限制在 0.0 到 0.05 之间的小范围内。

经过平方，重映射的粗糙度给出的结果在视觉上很直观，对于实时渲染来说也很友好。但是也要注意，由于计算中经常需要 Roughness 项，因此计算时浮点数的精度问题需要予以重视。比如 mediump 精度的 float 在移动 GPU 上一般会作为半精度也就是 FP16 来实现。

这样就会造成问题，比如计算 GGX 项中的 $\frac{1}{perceptualRoughness^4}$ 时，由于半精度浮点数可表示的最小值为 $2^{-14 }$ 或 $6.1 × 10^{-5}$，在不支持非规格化的设备上为了避免除以 0，这一项的结果必须不小于 $6.1 × 10^{-5}$， 为此 Roughness 必须被 clamp 到 0.089，也就是 $6.274 × 10^{-5}$。

很多时候为了控制镜面高光处于一个更小的范围，Roughness 也需要 clamp 到一个安全的范围，对于较低的 Roughness 值，这种 clamp 还可以避免高光出现的锯齿。

关于游戏中浮点数相关的内容可以看一下这篇文章。

Reflectance

电介质
菲涅尔项依赖于法向的镜面反射率 $f_0$ ，对于电介质材质是消色差的，可以用灰度来描述。Filament 中使用 Moving Frostbite to PBR 中所提到的电介质表面对反射率进行重映射：
\[\begin{equation} f_0 = 0.16 * {reflectance}^2 \end{equation}\]

这种做法的目标是将 $f_0$ 映射到常见的电介质表面（约 4%）以及宝石（8% ~ 16%）的菲涅尔值的范围内。 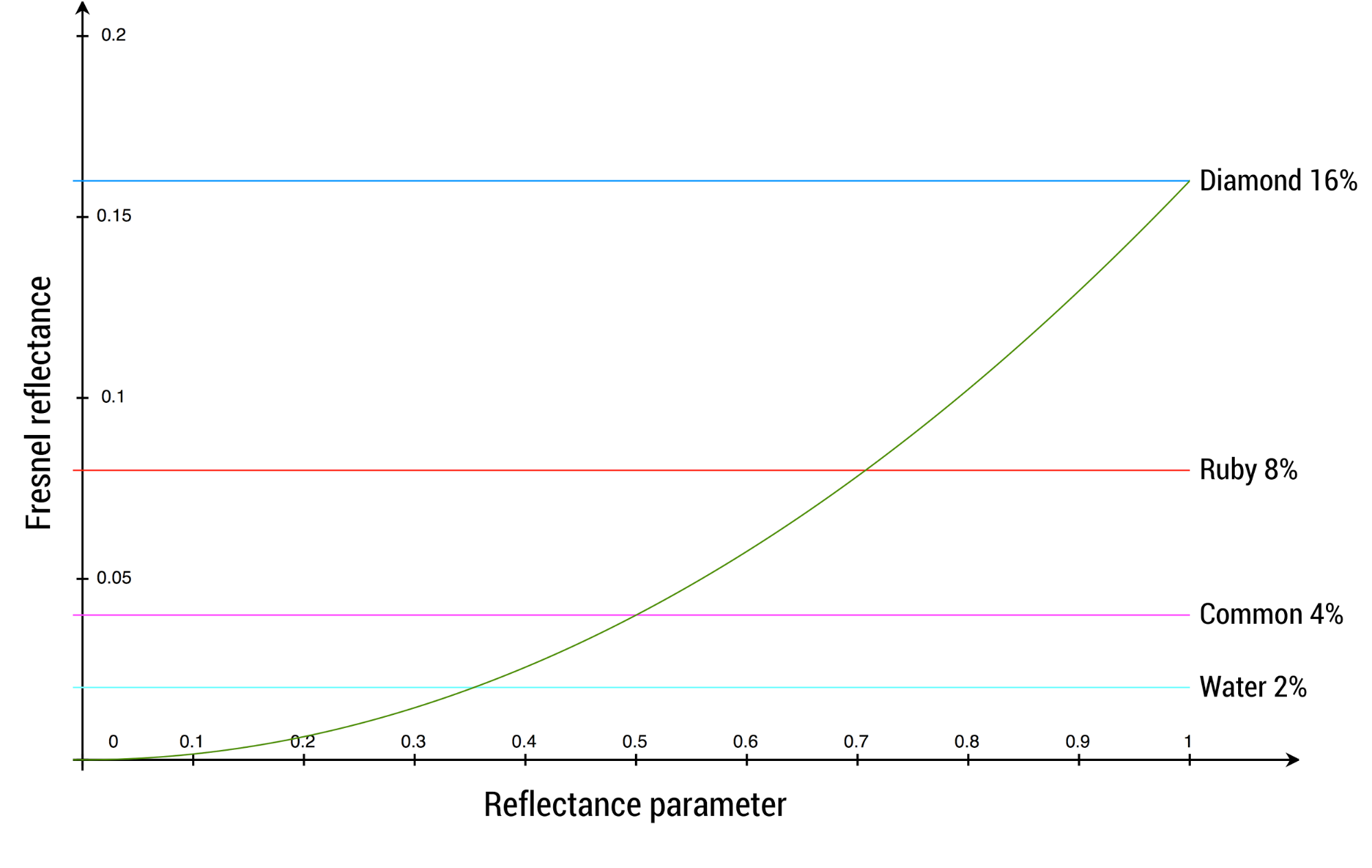Diagram_Reflectance 常见材质的反射率

假如折射率（IOR）已知，$f_0$ 可以做如下计算：

\[\begin{equation} f_0 = \frac{(n_{ior} - 1)^2}{(n_{ior} + 1)^2} \end{equation}\]

而假如反射率已知，也可以反求出其折射率：

\[\begin{equation} n_{ior} = \frac{2}{1 - \sqrt{f_0}} - 1 \end{equation}\]

下表中描述了自然界常见材质的菲涅尔反射率：

材料反射率折射率线性值
水2%1.330.35
织物4%~ 5.6%1.5~ 1.620.5~ 0.59
常见液体2%~ 4%1.33~ 1.50.35~ 0.5
常见宝石5%~ 16%1.58~ 2.330.56~ 1.0
塑料/玻璃4%~ 5%1.5~ 1.580.5~ 0.56
其他介电材料2%~ 5%1.33~ 1.580.35~ 0.56
眼睛2.5%1.380.39
皮肤2.8%1.40.42
头发4.6%1.550.54
牙齿5.8%1.630.6
默认4%1.50.5

在 Filament 中所有掠射角的反射率有 $F_{90} = 1.0$

导体
金属表面的镜面反射率不是消色的，是彩色的：
\[\begin{equation} f_0 = {baseColor}* {metallic} \end{equation}\]

对于电介质和金属材质而言，Filament 使用下面的方法计算 $f_0$:

1

vec3 f0 = 0.16 * reflectance * reflectance * (1.0 - metallic) + baseColor * metallic;

材质参考

Filament 提供了一个材质制作参考，帮助使用者制作自己的 PBR 材质。

对普通材质
BaseColor 应该没有除微表面的遮挡外的一切光照信息。金属度为非 0 即 1 的值，纯导体为 1，纯电介质为 0，因此对于这两类材质的金属度应该为接近 0 或 1的值，中间值应用于表面类型的过渡，如金属到铁锈。
对非金属材质
BaseColor 代表的是反射的颜色，应为 sRGB 50~ 240 或 sRGB 30~ 240。金属度应该为 0 或者接近 0 的值。反射率如果找不到合适的值，可以为 sRGB 127 (Linear 0.5， Reflectance 4%)。反射率不宜小于 sRGB 90（Linear 0.33，Reflectance 2%）
对金属材质
BaseColor 代表高光和反射的颜色，亮度应在 67%~ 100% (sRGB 170~ 255)，被氧化过或者更脏的金属可以考虑使用更低的值。金属度为 1 或者接近 1 的值。反射率可以被忽略，或由 BaseColor 计算而来。

参考

  1. Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs ↩

  2. Physically Based Shading at Disney ↩

3D, Graphics
3D rendering graphics material
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容

关于 Depth Buffer 的分布方式

Filament 材质篇（下）