Filament 材质篇（下）

本篇是 Filament 的笔记，以及部分自己的理解。

可以结合 Desktop 的渲染方式一起，看 Filament 的渲染为了更好地支持移动端，舍弃了哪些。

透明涂层（Clear coat）模型

这里把具有各向同性的单层材质称为标准材质，而标准材质上具有半透明薄膜涂层的，比如汽车油漆，漆木这类多层材料被称为透明涂层材质(Clear coat)

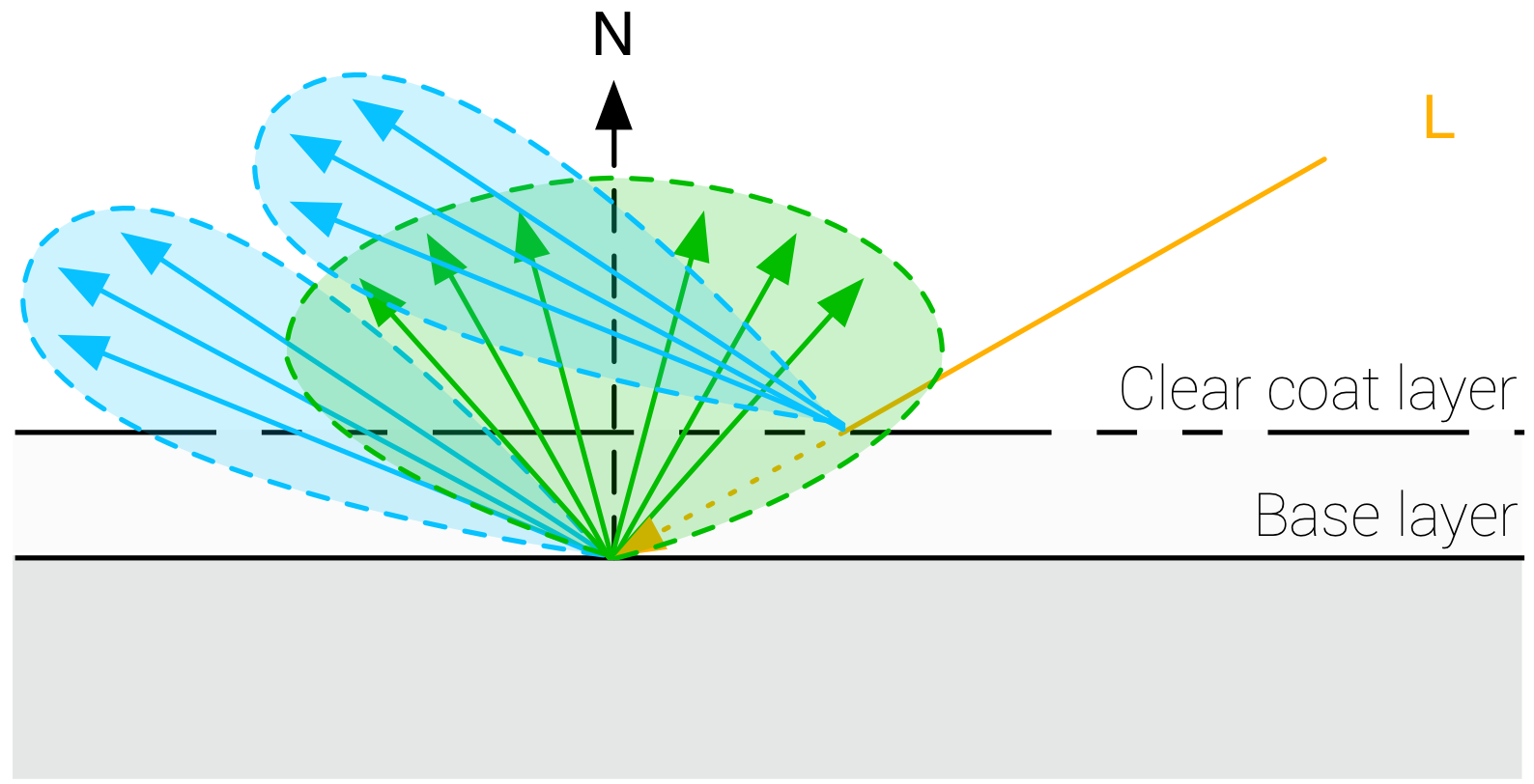
由上面的介绍可以看出，Clear coat 材质具有两层表面，其中标准材质层称为 Base layer，透明涂层称作 Clear coat layer，透明涂层是具有各向同性的电介质，标准材质层可以是任何层（电介质或导体）。Clear coat 材质的基本模型如下：

实时渲染领域，不会模拟涂层间的反射和折射行为，入射光将穿过透明涂层，因此也会存在能量损失。

Clear Coat Specular BRDF

Clear coat 也会使用标准模型中同样的 Cook-Torrance 微表面 BRDF 进行建模。由于透明涂层是具有各向同性的电介质，具有较低的粗糙度，因此可以选择比较简单的 D，F，G。

由于标准模型中使用的分布函数项以及菲涅尔项的计算已经足够简单¹²，所以这里仅考虑 Geomertry 项，在这篇论文³中描述了一种基于重要性采样的可以取代 SmithGGX 的几何阴影函数。

\[\begin{equation} V(l,h) = \frac{1}{4({l}\cdot{h})^2} \end{equation}\]

这个函数所描绘的 Mask Shadow 并不是基于物理的，但它足够简单，适合实时渲染。GLSL 中的实现也非常简单：

  
float V_Kelemen(float LoH) {
    return 0.25 / (LoH * LoH);
}

关于 Fresnel 项

Specular BRDF 需要法向的反射率 $f_0$，这里假定涂层的主要成分是聚氨酯，一种涂料和清漆中常见的化合物，在空气-聚氨酯的 IOR 为 1.5，因此可以参考上面提到的公式计算 $f_0$：

\[\begin{equation} f_0 = \frac{(1.5 - 1)^2}{(1.5 + 1)^2} = 0.04 \end{equation}\]

由于透明涂层的存在，必须考虑能量的损耗，

\[\begin{equation} f(v,l) = f_d(v,l)(1- F_c)+f_r(v,l)(1-F_c)+f_c(v,l) \end{equation}\]

这里，$F_c$ 是 clear coat 的 Fresnel 项，$f_c$ 是 clear coat BRDF。

参数

除了标准模型的 6 个参数（BaseColor, Roughness,Metallic,Reflectance，Emissive，Ambient occlusion）外，clear coat 添加了另外两个参数，

参数	定义
ClearCoat	透明涂层的强度，介于 0 到 1 之间。
ClearCoatRoughness	非物理真实的感知粗糙度，介于 0 到 1 之间。

ClearCoatRoughness 是重新映射的值，映射方法、clamp 的值域与标准模型的粗糙度一样，以开平方的方式再映射到线性空间。

ClearCoat 从 0 到 1 的变化，金属度 1.0，粗糙度 0.8

ClearCoatRoughness 从 0 到 1 的变化，金属度 1.0，粗糙度 0.8，ClearCoat 1.0

完成了再映射和参数化的、集成了 clear coat BRDF 的 GLSL 实现：

  
void BRDF(...) 
{
    // compute Fd and Fr from standard model

    // remapping and linearization of clear coat roughness
    clearCoatPerceptualRoughness = clamp(clearCoatPerceptualRoughness, 0.089, 1.0);
    clearCoatRoughness = clearCoatPerceptualRoughness * clearCoatPerceptualRoughness;

    // clear coat BRDF
    float  Dc = D_GGX(clearCoatRoughness, NoH);
    float  Vc = V_Kelemen(clearCoatRoughness, LoH);
    float  Fc = F_Schlick(0.04, LoH) * clearCoat; // clear coat strength
    float Frc = (Dc * Vc) * Fc;

    // account for energy loss in the base layer
    return color * ((Fd + Fr * (1.0 - Fc)) * (1.0 - Fc) + Frc);
}

标准材质层

涂层的存在使得反射的 $f_0$ 需要重新计算，因为原先的 $f_0$ 是基于空气-材质层的，而标准材质层需要计算的是材质-涂层这一层。我们可以用 $f_0$ 表示材质的折射率 $IOR_{base}$ 从而获得涂层的 $f_{0base}$。

首先计算标准材质层的 IOR:

\[\begin{equation} IOR_{base} = \frac{1+\sqrt{f_0}}{1-\sqrt{f_0}} \end{equation}\]

然后计算标准材质层的 $f_{0base}$，其中 1.5 是涂层的折射率，

\[\begin{equation} f_{0base} = (\frac{IOR_{base}-1.5}{IOR_{base}+1.5})^2 \end{equation}\]

涂层层的折射率是固定的，可以将上述的两个方程联立以简化：

\[\begin{equation} f_{0base} = \frac{(1-5\sqrt{f_0})^2}{(5-\sqrt{f_0})^2} \end{equation}\]

如果需要进一步的优化 clear coat 模型，可以将标准材质层的粗糙度从 ClearCoatRoughness 中分离出来。

各向异性模型

上面所描述的材质模型均是针对各项同性表面，即表面各个方向的属性是一样的。但是像是拉丝金属这类材质，需要用各向异性模型进行表达：

各向同性 vs 各向异性

各项异性 specular BRDF

可以通过将描述各向同性的标准材质模型的 specular BRDF 的粗糙度分解为切线方向的粗糙度 $\alpha_{t}$ 和副切线方向的粗糙度 $\alpha_{b}$，从而获得各向异性材质的 NDF

\[\begin{equation} D_{aniso}(h,\alpha) = \frac{1}{\pi\alpha_{t}\alpha_{b}} \frac{1}{(( \frac{t \cdot h}{\alpha_{t}})^2 + ( \frac{b \cdot h}{\alpha_{b}})^2 +(n \cdot h)^2)^2} \end{equation}\]

但是这个 NDF 会引入两个额外参数。Neubelt13⁴ 提出引入 anisotropy 参数，用该参数来表示 $\alpha_{t}$ 和 $\alpha_{b}$，

\[\begin{align*} \alpha_t &= \alpha \\ \alpha_b &= lerp(0, \alpha, 1 - anisotropy) \end{align*}\]

迪士尼的模型¹中定义的各向异性有较好的视觉效果，但也更为昂贵：

\[\begin{align*} \alpha_t &= \frac{\alpha}{\sqrt{1 - 0.9 \times anisotropy}} \\ \alpha_b &= \alpha \sqrt{1 - 0.9 \times anisotropy} \end{align*}\]

Filament 没有使用上面二者，而是选择了高光更为锐利的 Kulla17⁵:

\[\begin{align*} \alpha_t &= \alpha \times (1 + anisotropy) \\ \alpha_b &= \alpha \times (1 - anisotropy) \end{align*}\]

由于法线贴图本身就需要切线和副切线数据，因此这两个参数可以很方便的获得到，下面是最终的实现：

  
float at = max(roughness * (1.0 + anisotropy), 0.001);
float ab = max(roughness * (1.0 - anisotropy), 0.001);

float D_GGX_Anisotropic(float NoH, const vec3 h,
        const vec3 t, const vec3 b, float at, float ab) {
    float ToH = dot(t, h);
    float BoH = dot(b, h);
    float a2 = at * ab;
    highp vec3 v = vec3(ab * ToH, at * BoH, a2 * NoH);
    highp float v2 = dot(v, v);
    float w2 = a2 / v2;
    return a2 * w2 * w2 * (1.0 / PI);
}

参数

各向异性材质模型在标准材质的基础上多出了一项各向异性系数 Anisotropy，该参数为 -1 到 1 的标量，负值表示向副切线方向对齐，正值表示向切线方向对齐。

Anisotropy 从零到一的变化

布料模型

衣服、织物的布料通常由松散连接的丝线构成，这类材质会吸收和散射入射光。而微表面的 BRDF 模型假定材质表面有随机凹槽构成，在宏观上近似光滑平面，这导致微表面 BRDF 模型不太适合重建布料这种存在散射的材质。

传统微表面 BRDF 模型下的布料（左）与 Filament 中的布料（右）

像天鹅绒这类材质，由于布料表面直立的纤维会产生前向和后向的散射。前向散射指的是，入射光来自于观察向量的反方向的散射。而后向散射指的就是，入射光来自于观察向量相同方向的散射。

其他类型的布料，如皮革、丝绸等，更适合使用硬表面的材质模型，如标准模型或是各向异性模型。

布料的 Specular BRDF

Filament 使用的布料 BRDF 是经过修改的微表面 BRDF。而在 BRDF 的各项中，分布函数项（NDF）对 BRDF 的贡献最大⁶。该分布项是逆高斯分布，有助于实现前向/后向散射的模糊照明，并在此基础上添加模拟镜面反射的偏移。描述天鹅绒材质的 NDF 描述如下：

\[\begin{equation} D_{velvet}(v,h,\alpha) = c_{norm}(1 + 4 exp\left(\frac{-{cot}^2\theta_{h}}{\alpha ^2}\right)) \end{equation}\]

该 NDF 是 Ashikhmin00⁷ 中的变体，该 NDF 也有标准化的版本⁴：

\[\begin{equation} D_{velvet}(v,h,\alpha) = \frac{1}{\pi(1 + 4\alpha^2)}(1 + 4 \frac{exp\left(\frac{-{cot}^2\theta_{h}}{\alpha^2}\right)}{\sin^4{\theta_{h}}}) \end{equation}\]

标准化的等式中，分母可以进一步平滑为：

\[\begin{equation} f_{r}(v,h,\alpha) = \frac{D_{velvet}(v,h,\alpha)}{4(n \cdot l + n \cdot l - (n \cdot l)(n \cdot v))} \end{equation}\]

GLSL 的实现如下，适配了半浮点数并避免了余切的计算，用三角函数恒等式替换，且在该 BRDF 中删去了 Fresnel 项：

  
float D_Ashikhmin(float roughness, float NoH) 
{
    // Ashikhmin 2007, "Distribution-based BRDFs"
    float a2 = roughness * roughness;
    float cos2h = NoH * NoH;
    float sin2h = max(1.0 - cos2h, 0.0078125); // 2^(-14/2), so sin2h^2 > 0 in fp16
    float sin4h = sin2h * sin2h;
    float cot2 = -cos2h / (a2 * sin2h);
    return 1.0 / (PI * (4.0 * a2 + 1.0) * sin4h) * (4.0 * exp(cot2) + sin4h);
}

此外还有一种 NDF 的实现⁸，不同于前者使用了逆高斯分布的 NDF，该分布以正弦函数的指数为基础，它的参数表达更为自然直观，效果更加柔和，被称为Charlie Sheen。

\[\begin{equation} D(m) = \frac{(2+\frac{1}{\alpha})\sin(\theta)^\frac{1}{\alpha}}{2\pi} \end{equation}\]

Filament 中的优化实现如下：

  
float D_Charlie(float roughness, float NoH) 
{
    // Estevez and Kulla 2017, "Production Friendly Microfacet Sheen BRDF"
    float invAlpha  = 1.0 / roughness;
    float cos2h = NoH * NoH;
    float sin2h = max(1.0 - cos2h, 0.0078125); // 2^(-14/2), so sin2h^2 > 0 in fp16
    return (2.0 + invAlpha) * pow(sin2h, invAlpha * 0.5) / (2.0 * PI);
}

光泽颜色

为使美术更好控制布料材质的外观，引入了直接修改镜面反射率的光泽颜色（Sheen Color）：

无光泽（左） vs 有光泽（右）

布料的 Diffuse BRDF

Filament 中的布料材质模型的漫反射项依然依赖于 Lambertian Diffuse BRDF，在布料的 diffuse BRDF 中，它被修改为能量守恒且可以提供此表面散射的，虽然这些修改并不是基于严谨的物理真实的效果修改的，但是可以在一定程度上模拟光线在布料表面的散射和吸收。

没有散射项的 Diffuse BRDF 项如下：

\[\begin{equation} f_{d}(v,h) = \frac{c_{diff}}{\pi}(1 - F(v,h)) \end{equation}\]

这里的 $F(v,h)$ 是布料的 Specular BRDF 的 Fresnel 项，在实践中可以选择忽略 $1 - F(v,h)$ 这一项，Filament 文档中认为不值得为该项徒增成本。

次表面散射的效果以 Wrapped lighting⁹ 的方式实现，这种方法会修改漫反射函数以使表面法线和光照方向垂直的点不全为黑，以此来提高漫反射的对比度，从而模拟光线的散射行为。Filament 中以能量守恒的形式实现：

\[\begin{equation} f_{d}(v,h) = \frac{c_{diff}}{\pi}(1 - F(v,h)) \left< \frac{n \cdot l + w}{(1 + w)^2} \right> \left< c_{subsurface} + n \cdot l \right> \end{equation}\]

这里的 $w$ 即是描述漫反射光包裹几何体程度的值，介于 0 到 1 之间。为避免引入额外参数，Filament 将其固定为 $w$ = 0.5。Filament 里还提到一点，漫反射项不能乘以 $n \cdot l$，我的猜测是因为 Wrapped lighting 模拟了表面的漫反射后，光线的强度不再与表面法线和光照方向的夹角直接关联，因此不能直接乘。

白色的布料（左）vs 具有棕色次表面散射的白色布料（右）

完整的布料 BRDF 实现如下：

  
// specular BRDF
float D = distributionCloth(roughness, NoH);
float V = visibilityCloth(NoV, NoL);
vec3  F = sheenColor;
vec3 Fr = (D * V) * F;

// diffuse BRDF
float diffuse = diffuse(roughness, NoV, NoL, LoH);
#if defined(MATERIAL_HAS_SUBSURFACE_COLOR)
// energy conservative wrap diffuse
diffuse *= saturate((dot(n, light.l) + 0.5) / 2.25);
#endif
vec3 Fd = diffuse * pixel.diffuseColor;

#if defined(MATERIAL_HAS_SUBSURFACE_COLOR)
// cheap subsurface scatter
Fd *= saturate(subsurfaceColor + NoL);
vec3 color = Fd + Fr * NoL;
color *= (lightIntensity * lightAttenuation) * lightColor;
#else
vec3 color = Fd + Fr;
color *= (lightIntensity * lightAttenuation * NoL) * lightColor;
#endif

参数

布料模型不具有 Metallic 和 Reflectance 两个参数，额外添加了 Sheen 和 SubsurfaceColor 两个参数：

参数	定义
SheenColor	用于创建双色调镜面布料的镜面高光的颜色，默认为 0.04 以匹配标准反射率
SubsurfaceColor	通过材质散射和吸收后的漫反射颜色的色调

创建类似天鹅绒的材质时，BaseColor 可以设为纯黑或其他较暗的颜色，色度应该反映在 SheenColor 上。而像牛仔布、棉布这类材质，SheenColor 就可以使用基于 BaseColor 的亮度。

参考

physically-based-shading-on-mobile