首页 使用 PCA 方法创建有向包围盒（OBB）
文章
取消

使用 PCA 方法创建有向包围盒（OBB）

发表于 2022/11/23
作者 Yohiro
13 分钟阅读

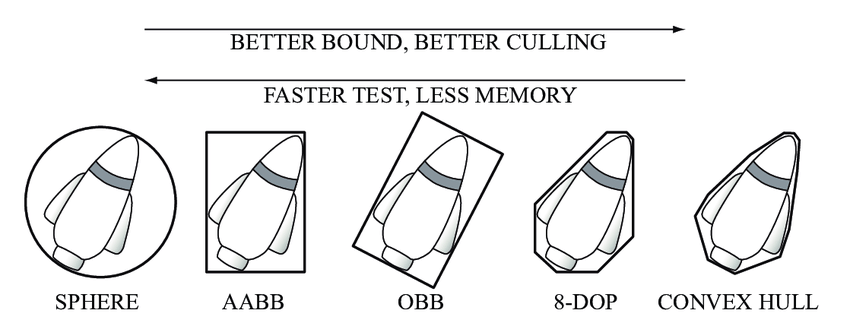
背景

在游戏开发中，常见的包围盒有球形包围盒、轴对齐包围盒（AABB）、有向包围盒（OBB）、K-DOP 以及凸包等，包围盒通常用于判断可见性以及碰撞检测等领域。其中，AABB 和 OBB 的应用最为广泛。

bounding-box 不同类型的包围盒

球形包围盒
球形包围盒是包含其所属对象的最小球体。一般用于较粗粒度的碰撞检测。
AABB (Axis-Aligned Bounding Box)
轴对齐包围盒（AABB） 是包含其所属对象的且各边平行于各坐标轴的最小六面体。它不会相对于轴进行旋转，因此可以仅通过 Min 和 Max 来进行定义，实现以及计算非常简单。但也由于不进行旋转，所以空间冗余很大。
OBB (Oriented Bounding Box)
定向包围盒（OBB）是包含其所属对象的且相对于坐标轴方向任意的最小的长方体。相较于 AABB，OBB 的空间利用率更高，但求交的时候也会变得复杂。
K-DOP (Discrete Oriented Polytope)
离散定向多面体 （DOP）是包含其所属对象的二维空间的凸多边形或者三维空间的凸多面体，它是一组无限远的定向平面移动到与物体相交而得到，于是 DOP 就是这些平面相交平面所生成的凸多面体。从 K 个平面构建的 DOP 称为 k-DOP。
凸包 (Convex Hull)
凸包是包容物体的最小凸体。如果物体是有限个点的集合，那么凸包就是一个多面体，实际上它是包容多面体的最小立体。

这篇文章主要用于阐述如何使用主成分分析（Principal Components Analysis）方法获得 OBB 的基向量，然后据此进一步创建 OBB。

PCA 介绍以及原理

想象一下在二维平面上有一系列的点，我们需要找到这些点分布最为零散的两个方向，且有尽可能多的点（的投影）在这两个方向上。这里我们要找的这两个方向实际上就是主成分，也是 OBB 的基向量。

介绍

主成分分析是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分。简单来讲，PCA 解决了这样一个问题：

如果我们有一组N维向量，现在要将其降到K维（K小于N），那么我们应该如何选择K个基才能最大程度保留原有的信息？

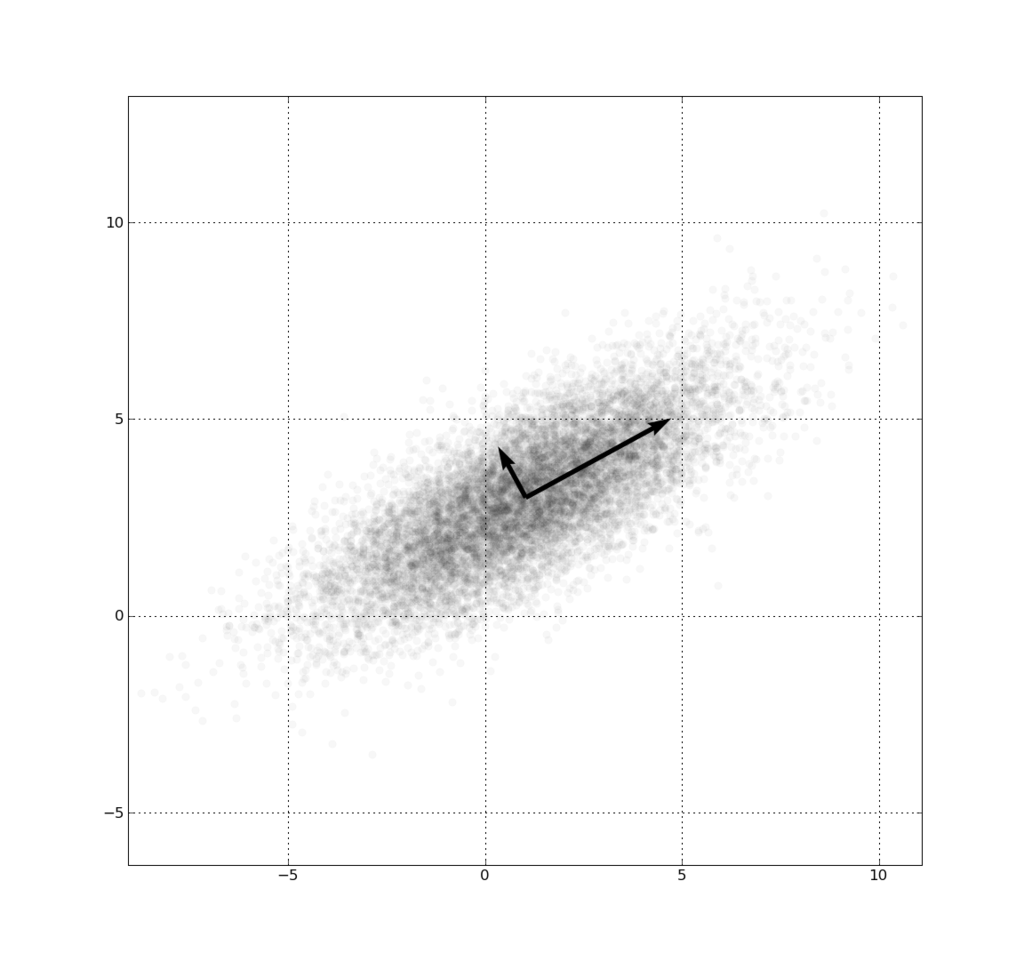PCA 一个高斯分布的主成分分析。黑色的两个向量是此分布的协方差矩阵的特征向量，其长度为对应的特征值之平方根，并以分布的平均值为原点。

原理

PCA 中的主成分实际上指的是，使数据中的点的投影数量最多的向量，这个向量被称作主成分。

那么如何找到主成分呢？这里来回顾一下数理统计和线性代数的内容。

在统计学里，方差（Variance）用于描述数据的离散程度，协方差（Covariance）用于描述数据的相关程度。方差越大，数据越离散；协方差越大，样本的相关性越强。

Covariance Trends

对于一维的数据，只需要找出方差最大的方向即可，这个方向就是一维数据的主成分，但对于更高维度的数据就需要引入协方差来解决。

对期望为 $E(X)$ 和 $E(Y)$ 的随机变量 $X$ 和 $Y$ 的协方差 $Cov(X,Y)$ 定义如下：

\[\begin{equation} Cov(X,Y) = E[(X-E(X))(Y-E(Y))] = E(XY) - E(X)E(Y) \end{equation}\]

从上式可知，$Cov(X,Y) = Cov(Y,X)$。

接下来要通过协方差来确定线性无关的方向，也就是独立的方向作为主成分。

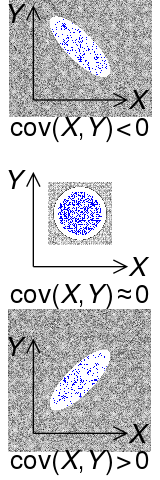
参考右图，当 $Cov(X,Y) > 0$ 时，两变量线性正相关；当 $Cov(X,Y) < 0$ 时，两变量线性负相关。 而当 $Cov(X,Y) == 0$ 时，两变量线性无关。

假设我们的数据是三维的，通过计算各维度数据的协方差后，可以得到这样的一个实对称矩阵，也就是协方差矩阵：

\[\begin{bmatrix} Cov(X,X) & Cov(X,Y) & Cov(X,Z) \\ Cov(Y,X) & Cov(Y,Y) & Cov(Y,Z) \\ Cov(Z,X) & Cov(Z,Y) & Cov(Z,Z) \\ \end{bmatrix}\]

主对角线的元素是变量与其自身的协方差，代表该变量的方差，非对角线上的元素代表协方差。

要找线性无关的方向，就要使协方差等于零，就需要令协方差矩阵的非对角线位置的值为零。因此，我们需要对协方差矩阵做变换，使非对角线上的元素化为零, 也就是将协方差矩阵对角化。

由于协方差矩阵是一个实对称矩阵，因此它具有以下性质：

  • 实对称矩阵的不同特征值所对应的特征向量是正交的
  • n 阶实对称矩阵必可对角化
  • k 重特征值必有 k 个线性无关的特征向量

也就是说，对于三维向量所构成的协方差矩阵，必然存在三个正交的特征向量，而这三个特征向量正是 OBB 的基向量，也就是 OBB 本地坐标系的轴。

那么接下来的问题就是如何将协方差矩阵对角化，求得特征向量。

求解特征向量，可以参考 Jacobi 迭代法，也可以调用其他三方数学库，如 Eigen。

通过以上步骤便获得了主成分，也就是 OBB 的基向量，更详细的数学解释可以阅读这篇文章。

算法

  1. 获得模型的顶点作为输入样本集
  2. 对样本集中的每一个样本点，计算协方差矩阵
  3. 求解协方差矩阵的特征向量
  4. 对样本集中的每一个样本点，计算样本点在特征向量方向上的投影距离，以获得 OBB 在各轴向上的最大和最小值
  5. 将上一步得到的 OBB 坐标系下的数据转换到世界坐标系下

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

void PCA(samples, x, y, z)
{
    // 期望
    vec3 center = 0
    for p in samples:
        center += p
    center /= samples.size()

    // 协方差矩阵
    matrix3x3 Covmatrix
    for p in samples:
        Covmatrix[0][0] += (p.x - center.x) * (p.x - center.x)
        Covmatrix[1][0] += (p.x - center.x) * (p.y - center.y)
        Covmatrix[2][0] += (p.x - center.x) * (p.z - center.z)

        Covmatrix[0][1] += (p.y - center.y) * (p.x - center.x)
        Covmatrix[1][1] += (p.y - center.y) * (p.y - center.y)
        Covmatrix[2][1] += (p.y - center.y) * (p.z - center.z)

        Covmatrix[0][2] += (p.z - center.z) * (p.x - center.x)
        Covmatrix[1][2] += (p.z - center.z) * (p.y - center.y)
        Covmatrix[2][2] += (p.z - center.z) * (p.z - center.z)

    // 将协方差矩阵归一化
    for elem in Covmatrix
        elem /= samples.size()

    // 求解协方差矩阵的特征向量矩阵
    matrix3x3 eigenVectors = computeEigenVectors(Covmatrix)
    vec3 lambda0 = eigenVectors.getColVector(0).normalize()
    vec3 lambda1 = eigenVectors.getColVector(1).normalize()
    vec3 lambda2 = eigenVectors.getColVector(2).normalize()

    // 获得 OBB 坐标系下的各轴向上的最大和最小值
    vec3 min,max
    for p in samples:
        vec3 local = p - center
        local = vec3(
            dot(local, lambda0),
            dot(local, lambda1),
            dot(local, lambda2)
        )

        min.x = min(local.x, min.x)
        min.y = min(local.y, min.y)
        min.z = min(local.z, min.z)
        
        max.x = max(local.x, max.x)
        max.y = max(local.y, max.y)
        max.z = max(local.z, max.z)

    vec3 localCenter = (min + max) * 0.5
    vec3 localExtent = (max - min) * 0.5
    
    // 变换到世界坐标系下
    vec3 worldCenter = center + lambda0 * localCenter.x + lambda1 * localCenter.y + lambda2 * localCenter.z 
    x = lambda0 * localExtent.x
    y = lambda1 * localExtent.y
    z = lambda2 * localExtent.z
    
    ...
}

其他

我的目的是通过 PCA 方法找到 OBB 的基，到这一步我已经达成目标了。但如果是使用 PCA 做数据降维，需要在上述取得特征向量后，将原始数据转换到以特征向量为基的数据空间内。假设我们要取 N 维数据，那么需要将特征向量按照其特征值的大小降序排列为矩阵，取前 N 行构成矩阵 P。那么，对于原数据 X 降至 N 维后的数据便是：

\[Y = PX\]

总结

PCA 本质上是将方差最大的方向作为数据的主要特征（基），从几何方面看，它能够选择数据最离散的方向构建无关的正交的向量，正是因为这点，我们可以使用该算法得到 OBB。而在数理统计方面，它可以作为一种简化数据集的方法来处理复杂数据，比如用在人脸识别方面。

但 PCA 假定主成分分布在正交的方向上，对于生成 OBB 没什么问题，但对于在非正交方向上方差较大的数据集，效果会很有限。

参考

Algorithm
geomertry engine algorithm math
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容

Delta Color Compression

Occlusion Cull