背景
我们现在玩的游戏,通常会使用 D24S8 格式的 DepthStencil,即深度占 24 位,模板占 8 位,深度用来存储像素前后的遮挡关系,模板用于标记具体的像素,这种格式可以兼顾精度还有性能,因此适用于绝大多数情况。但是我们在游戏开发中时还是会遇到由于 Depth Buffer 的精度不足而造成的前后的面片闪烁,即 Z-fighting 问题。
有很多种解决这个问题的方式,包括但不限于:
- 手动调整物件的纵深位置,通常是调整坐标 Z
- 轻微调整相机近平面的位置
- …
我们知道,屏幕空间中的 Z 值将会映射到深度 d 中,深度 d 在 DirectX 环境下被映射到 [0.0, 1.0],在 OpenGL 环境下被映射到 [-1.0, 1.0],这就是我们所谓的 NDC。
深度 depth_buffer_value 的值可以这样描述:
1
depth_buffer_value = (1<<N) * ( a + b / z );
其中,
1
2
3
4
N = number of bits of Z precision
a = zFar / ( zFar - zNear );
b = zFar * zNear / ( zNear - zFar );
z = distance from the eye to the object
这就使得深度值与 $\frac{1}{z}$ 成正比,即 depth_buffer_value 越小。具体表现为,越远的物体其精度越小,越近的物体精度越大。
因此,对于渲染 API 而言,它们期望投影矩阵中含有 $\frac{1}{z}$ 项,因为当投影矩阵中含有 $\frac{1}{z}$ 的前提下,透视才是正确的。
Reverse-Z
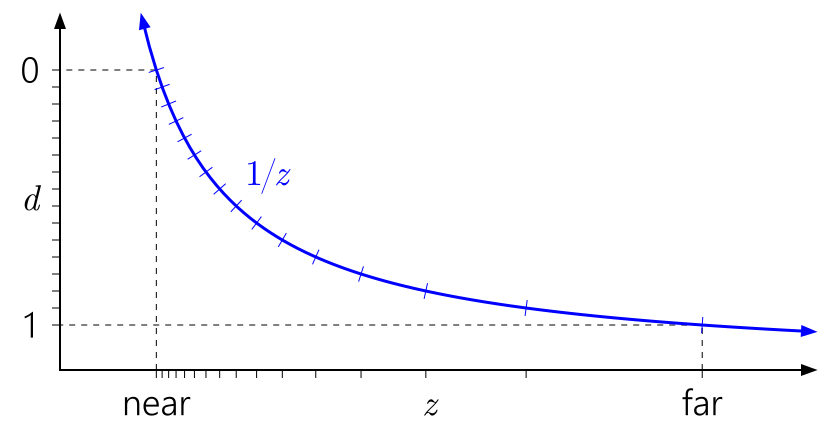
上图使用了整数的 z,可以看出 z 越远,d 的排布越稀疏,精度越低。
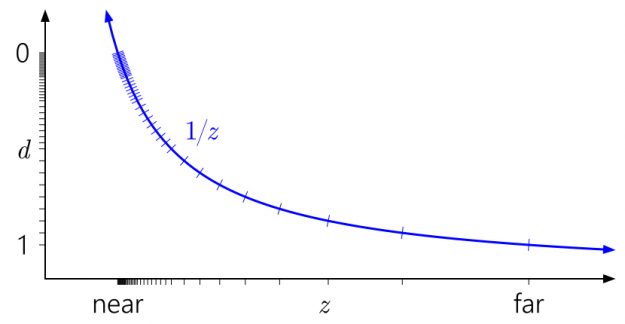
而上图使用浮点数 z 的情况则更为极端,可以看出精度绝大多数集中在了近平面一侧。
从上面的两张图可以看出,直接使用这种分布会使得精度的分布不均匀,导致了精度的浪费。既然精度集中在近平面一侧,那么将深度颠倒,令 1.0 是近平面,0.0 是远平面如何?
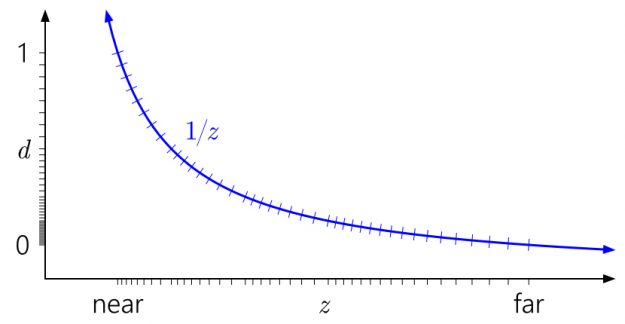
因此有所谓的 reverse-z 即反转 d 到 [1.0, 0.0] 的分布方式:
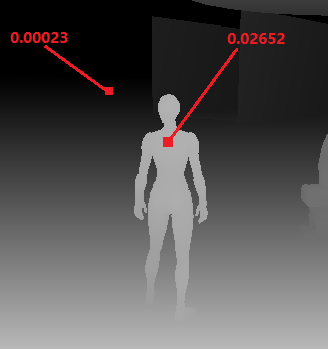
这种分布精度的分布比较均匀,越靠近近平面,depth 越接近 1.0。Unreal 中的 SceneDepthZ 就使用了这种分布方式:
Logarithmic 分布1
在这篇文章中提到了一种不同于 Reserve-Z 的,使用对数函数来映射深度的方式。
1
2
float Fcoef = 2.0 / log2(farplane + 1.0);
gl_Position.z = log2(max(1e-6, 1.0 + gl_Position.w)) * Fcoef - 1.0;
但是这种方式会因为最终输出的深度与 $\frac{1}{z}$ 不成正比,从而造成透视不正确。
为修复这一问题需要在 Pixel Shader 中修改深度2,这会导致 EarlyZ Test 失效,所以我认为这种分布方式不适用于游戏引擎这种对实时性要求较高的系统。
扩展阅读
- 图片来自 Visualizing Depth Precision
- Learning to Love your Z-buffer
- Tip of the day: logarithmic zbuffer artifacts fix
- Maximizing Depth Buffer Range and Precision
- Attack of the depth buffer
- density-of-floating-point-number-magnitude-of-the-number