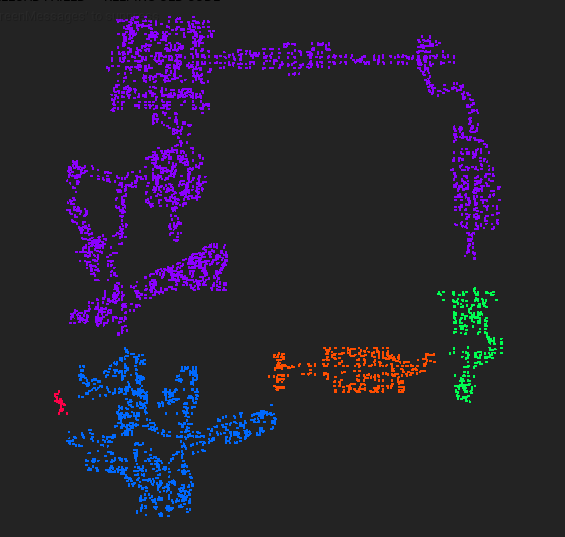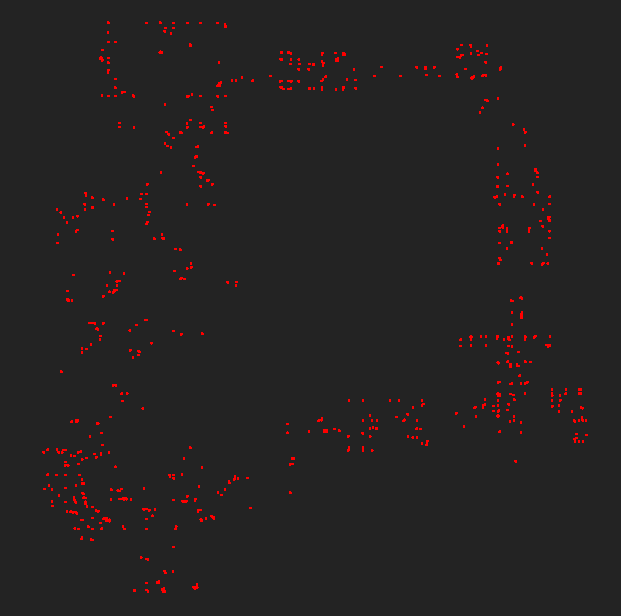介绍
在上一篇文章中介绍了 DBSCAN 的原理，这里来记录一下在引擎中的应用。
我决定引入聚类算法是为了尝试在 UE 中将放置某种包围盒的步骤自动化，从而提高迭代效率。
我在场景中沿着 Nav Mesh 生成了采样点，采样点的数量为 4643 个，分布如下：
可以视作采样点的集合 D
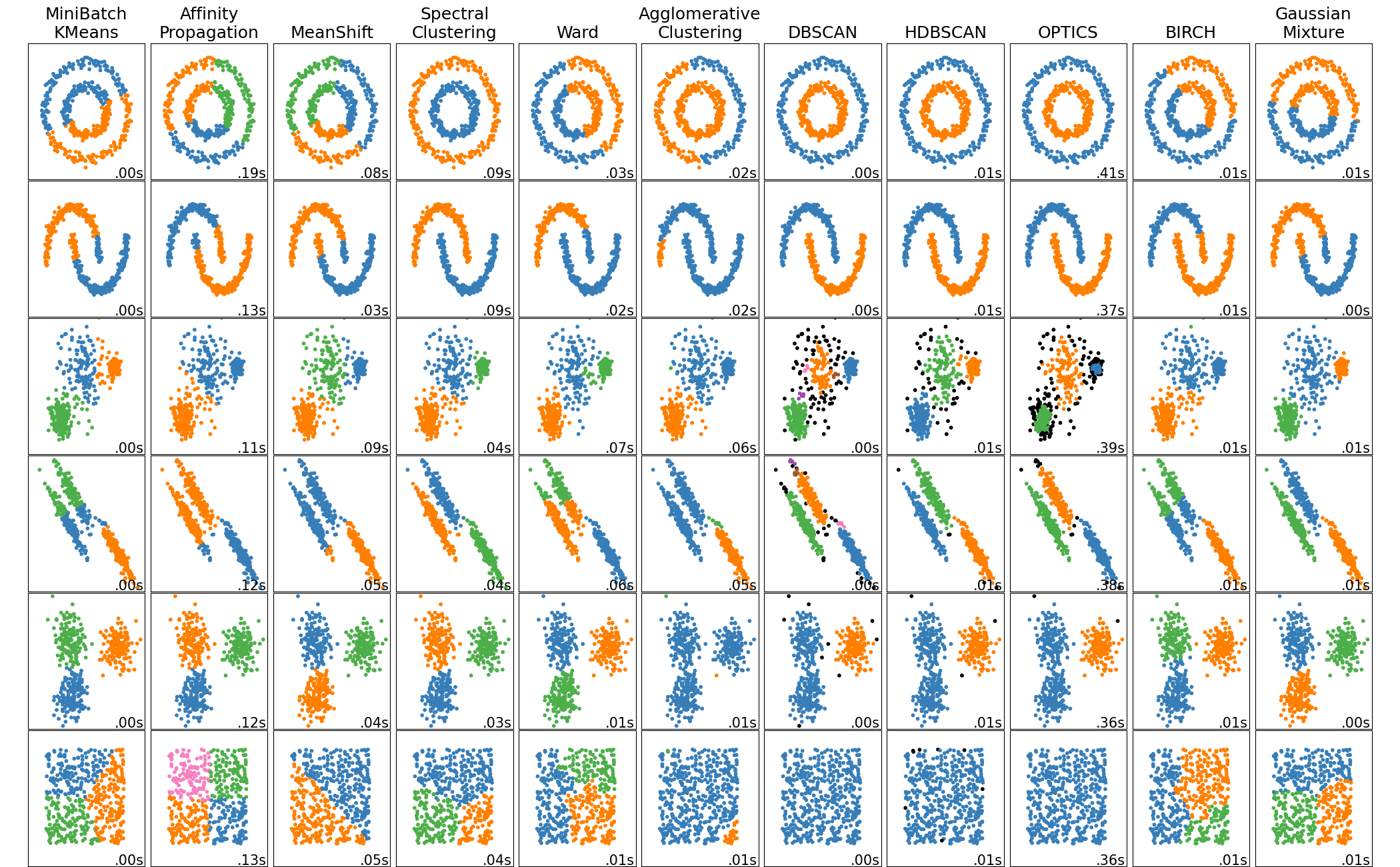
在参照下图对其他聚类算法进行了一些对比后，选择了使用 DBSCAN。
各种聚类算法的效果对比
这个选择出于以下几个原因：
- 采样点是沿着 Nav Mesh 生成的，密度比较平均
- DBSCAN 的算法比较简单，易于实现
- 游戏中的路径形成的样本集有可能是非凸的
- 噪声多可以接受，身是可以通过去除噪声点而达到离线构建效率优化的目的
综上，我选择了 DBSCAN。
参数选择
之前的文章中提到过参数选择的问题，原论文中介绍了一种叫做 k-dist 的选择 Epsilon 和 MinPts 的方法。
k-dist
k-dist 指的是样本中的点 P 到距它第 k 近的点的距离。通过排序后的 k-dist 图可以确定在哪个点（附近）距离变化速度大，从而了解密度分布的情况。
k-dist 方法是一种经验性的方法，试想这样一种情景：
设点 p 第 k 近的邻接点的距离为 d，那么对于半径为 d 的点 p 邻域内必包含至少 k+1 个点，这么说是因为邻域可能存在多个点到 p 的距离与 d 相同，对于大样本集，这种情况的概率较低，因此，可以认为点 p 的邻域 d 内包含 k+1 个点。
这时如果我们在样本集内选择任意一点 p，并将 Epsilon 设为上面提到的 d，将 MinPts 设为 k，则所有 k-dist 小于等于 d 的点都将成为核心点。
假如能够在最小的 Cluster 中找到最大的 k-dist 的值，便可确认以最小的 Cluster 的密度为参考的 Epsilon 阈值，这个值正是按照 k-dist 排序后的第一个拐点。
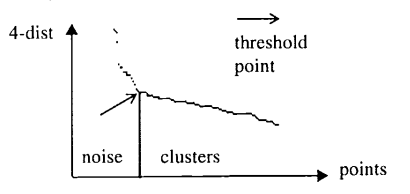以该拐点为界，左侧的点为噪声点，右侧的点为 Cluster 中的点
相对于该拐点，具有较大 k-dist 的值的点可以被认为是噪声点，所有其他较小的点则归于某个 Cluster。
步骤
假如数据集中的数据为 $N$ 维数据：
- 选取 k 值，可以取 k 为 $2N$ 或 $2N-1$
- 对数据集中所有的点 p，计算距离点 p 第 k 近的点的距离（k-distance）
- 依据 k-distance 的大小，将所有的点降序排序
- 绘制 k-distance 图
- 找到拐点位置的 k-dist 值，即为 Eps 的值。
- 取 Minpts 为 k+1
实现参考
这里我找到了 SimpleDBSCAN，一个轻量的 header-only 的 C++ 实现。SimpleDBSCAN 的实现中使用了 kd 树来做复杂的样本划分，以加速大样本的查询。
最终效果
使用 DBSCAN 进行聚类的结果如下，其中 MinPts = 10, Epsilon = 450:
| 聚类结果 | 噪声 |
 |  |
就该结果而言，存在下面几个问题：
- 聚类可以进一步细分，比如最上面连成一大块的紫色可以进一步划分
- 对于比较狭窄的地方，由于采样点不足，无法形成有效聚类，从而产生噪声
- 对于比较宽阔的地方，由于采样点之间的距离比较大，无法形成有效聚类，从而产生噪声
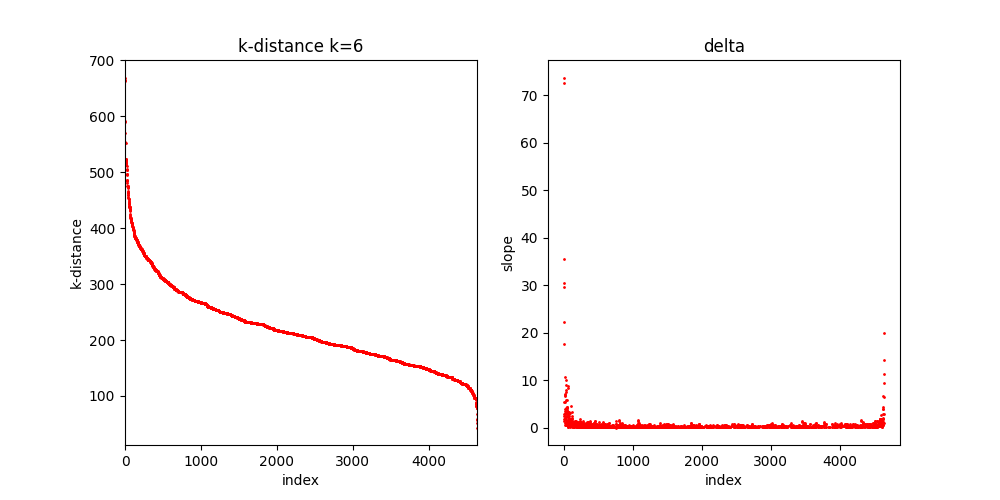
在引擎中导出 k-distance 数据后，使用 pyplot 绘制图像如下：
由于样本点数目较多，因此很难直观地看出拐点在哪里，这种情况下 k-dist 方法似乎不适用？从上图中可以得到的信息是，在大概 [280,380] 这个范围内 k-dist 变化较快，也就是说在 [280,380] 之外的区域即使调整 Eps 也不会有明显变化。
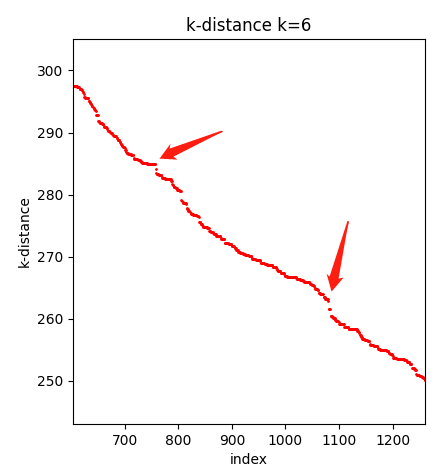
放大看了一下，最终我选择了 Eps = 288，下面是 MinPts = 6, Epsilon = 288 的结果：
| 聚类结果 | 噪声 |
 |  |
最终的结果差强人意，但基本满足了我的需求。
我也试了其他的参数，下面是 MinPts = 10, Epsilon = 350 的结果：
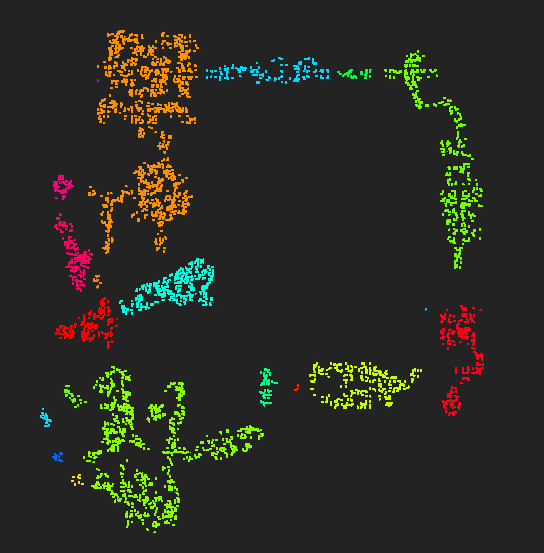MinPts = 10, Epsilon = 350 的划分结果
可以看到零碎的区域明显减少，因为随着 MinPts 和 Epsilon 的增大，划分 Cluster 的粒度逐渐变大。如果样本集中的密度相对平均，而又期望划分较大粒度的 Cluster，那么使用 k-dist 方法未必能直接获得结果，但是可以确定大致的范围，对样本的密度分布有一个直观的认识。
总结
使用 k-dist 可以确定 DBSCAN 的参数的范围，但实际应用中最好还是搭配可视化的数据调试界面进行参数的调整。而且 k-dist 找的是适配最小的 Cluster 的一组参数，有些情况下，我们会期望划分的 Cluster 具有较大的粒度，这种情况下使用 DBSCAN 或者 k-dist 方法确定参数可能不是那么合适了，或许 HDBSCAN 和 OPTICS 可以获得更好的结果。